支持向量机

• SVM（Support Vector Machine）：支持向量机
• SVC（Support Vector Classifier）：支持向量分类器
• SVR（Support Vector Regression）：支持向量回归器

支持向量机基本型

给定大小为 $m$ 的训练集 $D=\{(\mathbf{x}_1, y_1), (\mathbf{x}_2, y_2), \ldots, (\mathbf{x}_m, y_m)\},y_i\in\{-1, 1\}$。基于训练集 $D$ 在样本空间中找到一个超平面，将不同类别的样本分开，如下图：

明显红色的划分超平面更合适。划分超平面可通过线性方程描述：

$w^T\mathbf{x}+b=0$

• $w=(w_1, w_2, \ldots, w_n)$：为法向量，决定了超平面的方向；
• $b$：位移项。
• $\mathbf{x}=(\mathbf{x}_1, \mathbf{x}_2, \ldots,\mathbf{x}_n)$

样本空间中任意点到超平面 $(w,b)$ 的距离为：

$r=\frac{\vert w^T\mathbf{x}+b\vert}{\vert\vert w\vert\vert}$

在做分类时，应有 $(\mathbf{x}_i, y_i)\in D$，当 $y_i=+1$ 时，$w^T\mathbf{x}_i+b>0$；当 $y_i=-1$ 时，$w^T\mathbf{x}_i+b<0$。令：

$\begin{cases} w^T\mathbf{x}_i+b\geq+1, y_i=+1\\ w^T\mathbf{x}_i+b\leq-1, y_i=-1 \end{cases}$

距离超平面最近的几个训练样本点满足上式，如下图 $H_1$、$H_2$ 上的样本被称为支持向量（support vector）。

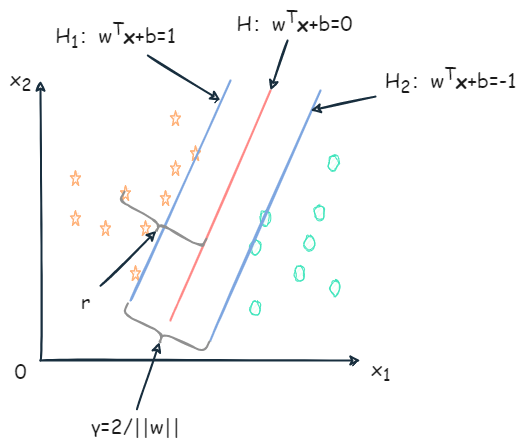
两个异类的支持向量到超平面的距离之和（也称为间隔）为：

$\gamma=\frac{\vert(b+1)-(b-1)\vert}{\vert\vert w\vert\vert}=\frac{2}{\vert\vert w\vert\vert}$

为了找到具有最大间隔的划分超平面，需要满足下式中约束参数 $w$ 和b，使得 $\gamma$ 最大：

$\max_{w,b}\frac{2}{\vert\vert w\vert\vert}\\ 同时保证\ y_i(w^T\mathbf{x}_i+b)\geq 1,i=1,2,\ldots,m.$

为了最大化间隔，需要最大化 $\vert\vert w\vert\vert^{-1}$，等价于最小化 $\vert\vert w\vert\vert^2$

$\min_{w,b}\frac{1}{2}\vert\vert w\vert\vert^2\\ 同时保证\ y_i(w^T\mathbf{x}_i+b)\geq 1,i=1,2,\ldots,m.$

对上式使用拉格朗日乘子法可得到它的对偶问题。

• 拉格朗日乘⼦法是⼀种寻找多元函数在⼀组约束下的极值的方法。

  • 通过引⼊拉格朗日乘子，可将有 $d$ 个变量与 $k$ 个约束条件的最优化问题转化为具有 $d+k$ 个变量的⽆约束优化问题求解。

• 对上式每条约束添加拉格朗日乘子 $\alpha_i\geq 0$

• 对偶问题是原始问题的一种变换形式，它在数学上与原始问题密切相关，但可能具有不同的结构和性质。

$L(w,b,\mathcal{\alpha})=\frac{1}{2}\vert\vert w\vert\vert^2+\sum_{i=1}^m\alpha_i(1-y_i(w^T\mathbf{x}_i+b))$

• 其中 $\mathcal{\alpha}=(\alpha_1, \alpha_2, \ldots, \alpha_m)$

令 $L(w,b,\mathcal{\alpha})$ 对 $w$ 和 $b$ 的偏导为零，可得

$\frac{\partial L(w,b,\mathcal{\alpha})}{\partial w}=w-\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i=0\Rightarrow w=\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i$

$\frac{\partial L(w,b,\mathcal{\alpha})}{\partial b}=-\sum_{i=1}^m\alpha_iy_i=0\Rightarrow 0=\sum_{i=1}^m\alpha_iy_i$

将 $w=\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i$ 代入 $L(w,b,\mathcal{\alpha})$，将 $w$ 和 $b$ 消去，再结合 $0=\sum_{i=1}^m\alpha_iy_i$，得到 $\min_{w,b}\frac{1}{2}\vert\vert w\vert\vert^2$ 的对偶问题：

$\max_{\mathcal{\alpha}}\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j\tag{1}$

$同时保证\ \sum_{i=1}^m\alpha_iy_i=0,\\ \alpha_i\geq0,i=1,2,\ldots,m.$

求解出 $\mathcal{\alpha}$ 后：

$f(\mathbf{x})=w^T\mathbf{x}+b=\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i^T\mathbf{x}+b\tag{2}$

上述过程需满足 KKT 条件，即：

$\begin{cases} \alpha_i\geq 0\\ y_if(\mathbf{x})-1\geq 0\\ \alpha_i(y_if(\mathbf{x})-1)=0 \end{cases}$

对任意训练样本 $(\mathbf{x}_i,y_i)$，总有 $\alpha_i=0$ 或 $y_if(\mathbf{x}_i)=1$。

• 若 $\alpha_i=0$，该样本不会出现在式 1 的求和中，也不会对 $f(\mathbf{x}_i)$ 产生影响。
• 若 $\alpha_i>0$，则必有 $y_if(\mathbf{x}_i)=1$，对应的样本点位于最大间隔边界上，即支持向量。

训练完后，大部分训练样本也不需要保留，最终模型仅与支持向量有关。

SMO

对于式 1 的求解，可以使用二次规划算法求解，也可以通过 SMO（Sequential Minimal Optimization） 算法求解。

SMO 的基本思路：

• 固定 $\alpha_i$ 之外的所有参数，求 $\alpha_i$ 上的极值。

• 每次选择两个变量 $\alpha_i$ 和 $\alpha_j$，同时固定其他参数，在参数初始化后，不断执行以下步骤直至收敛：

  • 选取一对需更新的变量 $\alpha_i$ 和 $\alpha_j$；
  • 固定 $\alpha_i$ 和 $\alpha_j$ 以外的参数，求解式 1 获得更新后的 $\alpha_i$ 和 $\alpha_j$ 。

  SMO 使选取的两变量所对应样本之间的间隔最大。

  • 使得两个变量有很大区别，给目标函数值更大的变化。

核函数

上述讨论训练样本是线性可分的（即存在划分超平面能正确分类），如果原始样本空间内不能存在这样的划分超平面，那么需要 将样本从原始空间映射到更高维的空间，使其在这个特征空间内线性可分。

• 令 $\phi(\mathbf{x})$ 表示将 $\mathbf{x}$ 映射后的特征向量，则在特征空间中划分超平面所对应的模型表示为：

$f(\mathbf{x})=w^T\phi(\mathbf{x})+b$

其中 $w$ 和 $b$ 为模型参数，有：

$\min_{w,b}\frac{1}{2}\vert\vert w\vert\vert^2\\ 同时保证\ y_i(w^T\phi(\mathbf{x}_i)+b)\geq 1,\ i=1,2,\ldots,m$

其对偶问题是：

$\max_\alpha\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j)\\ 同时保证\ \sum_{i=1}^m\alpha_iy_i=0,\alpha_i\geq 0,i=1,2,\ldots,m$

设计核函数：

$\kappa(\mathbf{x}_i, \mathbf{x}_j)=<\phi(\mathbf{x}_i),\phi(\mathbf{x}_j)>=\phi(\mathbf{x}_i)^T\phi(\mathbf{x}_j)$

• 即 $\mathbf{x}_i$ 与 $\mathbf{x}_j$ 在特征空间的内积等于它们在原始样本空间通过函数 $\kappa(\cdot,\cdot)$ 计算的结果。

所以之前的式子改写为：

$\max_\alpha\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\kappa(\mathbf{x}_i,\mathbf{x}_j)\\ 同时保证\ \sum_{i=1}^m\alpha_iy_i=0,\alpha_i\geq 0,i=1,2,\ldots,m$

求解后可得到：

$f(\mathbf{x})=w^T\phi(\mathbf{x})+b\\ =\sum_{i=1}^m\alpha_iy_i\phi(\mathbf{x}_i)^T\phi(\mathbf{x})+b\\ =\sum_{i=1}^m\alpha_iy_i\kappa(\mathbf{x}_i,\mathbf{x})+b$

• 上式说明模型最优解可通过训练样本的核函数展开，展式称为支持向量展式。

定理：令 $\chi$ 为输入空间，$\kappa(\cdot,\cdot)$ 式定义在 $\chi\times\chi$ 上的对称函数，则 $\kappa$ 式核函数 当且仅当 对于任意数据 $D=\{\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_m\}$，核矩阵 $K$ 总是半正定的：

$K=\left[\begin{matrix} \kappa(\mathbf{x}_1,\mathbf{x}_1) & \cdots & \kappa(\mathbf{x}_1,\mathbf{x}_j) & \cdots & \kappa(\mathbf{x}_1,\mathbf{x}_m)\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ \kappa(\mathbf{x}_i,\mathbf{x}_1) & \cdots & \kappa(\mathbf{x}_i,\mathbf{x}_j) & \cdots & \kappa(\mathbf{x}_i,\mathbf{x}_m)\\ \vdots & \ddots & \vdots & \ddots & \vdots\\ \kappa(\mathbf{x}_m,\mathbf{x}_1) & \cdots & \kappa(\mathbf{x}_m,\mathbf{x}_j) & \cdots & \kappa(\mathbf{x}_m,\mathbf{x}_m) \end{matrix}\right]$

• 对于一个半正定和矩阵，总能找到一个与之对应的映射 $\phi$。任何一个核函数都隐式定义了一个称为“再生核希尔伯特空间”（简称RKHS）的特征空间。

常用核函数如下：

• 线性核：$\kappa(\mathbf{x}_i,\mathbf{x}_j)=\mathbf{x}_i^T\mathbf{x}_j$；
• 多项式核：$\kappa(\mathbf{x}_i,\mathbf{x}_j)=(\mathbf{x}_i^T\mathbf{x}_j)^d$，$d\geq 1$ 为多项式的次数；
• 高斯核：$\kappa(\mathbf{x}_i,\mathbf{x}_j)=\exp(-\frac{\vert\vert\mathbf{x}_i-\mathbf{x}_j\vert\vert^2}{2\sigma^2})$，$\sigma>0$ 为高斯核的带宽；
• 拉普拉斯核：$\kappa(\mathbf{x}_i,\mathbf{x}_j)=\exp(-\frac{\vert\vert\mathbf{x}_i-\mathbf{x}_j\vert\vert^2}{\sigma^2})$，$\sigma>0$；
• Sigmoid核：$\kappa(\mathbf{x}_i,\mathbf{x}_j)=\tanh(\beta\mathbf{x}_i^T\mathbf{x}_j+\theta)$，$\tanh$ 为双曲正切函数，$\beta>0,\theta<0$。

此外，核函数还可通过组合得到：

• 若 $\kappa_1$ 和 $\kappa_2$ 为核函数，则对于任意正数 $\gamma_1、\gamma_2$，其线性组合 $\gamma_1\kappa_1+\gamma_2\kappa_2$ 也是核函数。
• 若 $\kappa_1$ 和 $\kappa_2$ 为核函数，则核函数的直积 $\kappa_1\otimes\kappa_2(\mathbf{x}_i,\mathbf{z})=\kappa_1(\mathbf{x}_i,\mathbf{z})\kappa_2(\mathbf{x}_i,\mathbf{z})$ 也是核函数。
• 若 $\kappa_1$ 为核函数，则对于任意函数 $g(x)$，$\kappa(\mathbf{x},\mathbf{z})=g(\mathbf{x})\kappa_1(\mathbf{x},\mathbf{z})g(\mathbf{z})$ 也是核函数。

C-SVC算法

C-SVC算法：受参数 $C$ 的制约。

• 参数 $C$ 是最小的训练误差和最大的分类间隔的折中。
• 常用交叉验证法选取 $C$。

给定大小为 $m$ 的训练集 $D$，其中每个样本具有 $n$ 个属性，对应一个标签 $y_i\in\{+1,-1\}$ 表示其分类。

• $+1$ 表示正例
• $-1$ 表示负例

超平面方程表示为：

$w^T\mathbf{x}+b=0$

对每一个样本 $\mathbf{x}_i$，引入一个松弛变量 $\xi\geq 0$，作为错误分类误差的度量，可以被认为是在分类错误的情况下样本与属于它的间隔边界超平面的距离。

• 如果分类正确，该变量为0。

$\xi_i=\begin{cases}0,&如果\ y_i(w^T\mathbf{x}_i+b)\geq +1\\ 1-y_i(w^T\mathbf{x}_i+b),&如果\ y_i(w^T\mathbf{x}_i+b)\leq +1 \end{cases}$

由上式得到原公式下实现软间隔最大化的约束条件：

$y_i(w^T\mathbf{x}_i+b)\geq 1-\xi_i,\ \xi_i\geq 0,\ i=1,2,\ldots,m$

如下图 $H_1$ 和 $H_2$ 之间的间隔称为软间隔：

在软间隔最大化中，被软间隔分隔错误的样本应该受到惩罚，且随着 $\xi_i$ 增大而增加。还要尽可能减少错误分隔的样本数。软间隔最大化原公式如下：

$\min\frac{1}{2}\vert\vert w\vert\vert^2+C\sum_{i=1}^m\xi_i\\ 同时保证\ y_i(w^T\mathbf{x}_i+b)\geq 1-\xi_i,\ \xi_i\geq 0,i=1,2,\ldots,m$

• $C$ 为非负的惩罚参数，用于对分类错误样本的一定程度上的惩罚。
  • $C$ 大，相当于错误惩罚力度大。达到一定程度从而没有错误分类的样本，软间隔最大化等价于硬间隔最大化。
  • $C$ 小，相当于错误惩罚力度小。可能有更多样本被软间隔分类错误。
• $\sum_{i=1}^m\xi_i$ 为分类错误的总量。

对其进行构造拉格朗日方程：

$L(w,b,\mathcal{\alpha},\xi,\mu)=\frac{1}{2}\vert\vert w\vert\vert^2+\sum_{i=1}^m\alpha_i(1-y_i(w^T\mathbf{x}_i+b))+\sum_{i=1}^m(C-\alpha_i-\mu_i)\xi_i$

也求偏导得到

$\frac{\partial L(w,b,\mathcal{\alpha},\xi,\mu)}{\partial w}=w-\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i=0\Rightarrow w=\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i$

$\frac{\partial L(w,b,\mathcal{\alpha},\xi,\mu)}{\partial b}=-\sum_{i=1}^m\alpha_iy_i=0\Rightarrow 0=\sum_{i=1}^m\alpha_iy_i$

$\frac{\partial L(w,b,\mathcal{\alpha},\xi,\mu)}{\partial \xi_i}=C-\alpha_i-\mu_i=0$

最后通过偏导式、拉格朗日方程、原公式得到软间隔对偶优化问题：

$\max_\alpha-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\mathbf{x}_i^T\mathbf{x}_j+\sum_{i=1}^m\alpha_i\\ 同时保证\ \sum_{i=1}^m\alpha_iy_i=0和0\leq\alpha_i\leq C,\ i=1,2,\ldots,m$

KTT 条件：

$\alpha_i(y_i(w^T\mathbf{x}_i+b)-1+\xi_i)=0,\ (C-\alpha_i)\xi_i=0,\ i=1,2,\ldots,m$

• $\xi_i=0,\ \alpha_i=0$：样本被正确分类，并且这些样本不是支持向量，不影响最终解。
• $\xi_i=0,\ 0<\alpha_i<C$：样本在间隔超平面上，即这些向量是支持向量。
• $0<\xi_i\leq1,\ \alpha_i=C$：表示样本被分割超平面正确分类，但落在软间隔内。
• $\xi_i>1,\ \alpha_i=C$：样本被错误分类。

设 $\alpha^*=(\alpha_1^*,\alpha_2^*,\ldots,\alpha_m^*)$ 为解，得到分隔超平面的法向量 $w^*$ 为：

$w^*=\sum_{i=1}^m\alpha_i^*y_i\mathbf{x}_i$

然后通过 $\alpha_i(y_i(w^T\mathbf{x}_i+b)-1+\xi_i)=0,\ (C-\alpha_i)\xi_i=0,\ i=1,2,\ldots,m$ 计算 $b$，并把它的平均值作为分隔超平面的偏移量 $b^*$，则最终的决策函数为：

$f(\mathbf{x})=\mathbf{sgn}\left(\sum_{i=1}^m\alpha_i^*y_iK(\mathbf{x}_i\cdot\mathbf{x})+b^*\right)$

ν-SVC 算法

使用参数 $\nu$ 代替参数 $C$。

• 表示支持向量占全部训练样本的比例下限；
• 也表示错误分类样本占全部训练样本的比例上限。
• 如 $\nu=0.05$，则保证最多有5%的训练样本被错分类，且至少有5%的支持向量。

用常系数 $\nu$ 代替参数 $C$，同时还引入一个需要被优化的变量 $\rho$，ν-SVC 的原公式：

$\min\frac{1}{2}\vert\vert w\vert\vert^2-\nu\rho+\frac{1}{m}\sum_{i=1}^m\xi_i\\ 同时保证\ y_i(w^T\mathbf{x}_i+b)\geq\rho-\xi_i和\xi_i\geq 0,\rho\geq 0,i=1,2,\ldots,m$

ν-SVC 的软间隔宽度为：$2\rho/\vert\vert w\vert\vert$。

拉格朗日方程：

$L(w,b,\mathcal{\alpha},\xi,\mu,\rho,\delta)=\frac{1}{2}\vert\vert w\vert\vert^2-\nu\rho+\frac{1}{m}\sum_{i=1}^m\xi_i-\sum_{i=1}^m\alpha[y_i(w^T\mathbf{x}_i+b)-\rho+\xi_i]-\sum_{i=1}^m\mu\xi_i-\delta\rho$

再次求偏导，使导数为0，得到：

$w=\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i$

$\alpha_i+\mu_i=\frac{1}{m}$

$\sum_{i=1}^m\alpha_iy_i=0$

$\sum_{i=1}^m\alpha_i-\delta=0$

结合，最终得到二次优化问题：

$\max_\alpha-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jK(x_i,x_j)\\ 同时保证\ \sum_{i=1}^m\alpha_iy_i=0,0\leq\alpha_i\leq\frac{1}{m}和\sum_{i=1}^m\alpha_i\geq\nu,\ i=1,2,\ldots,m$

常系数 $\nu$ 仍需满足：

$\nu\leq\frac{2\min(\mathbf{Nums}(y_i=+1),\mathbf{Nums}(y_i=-1))}{m}$

• $\mathbf{Nums}(y_i=+1)$ 表示样本中正例数量。
• $\mathbf{Nums}(y_i=-1)$ 表示样本中负例数量。

决策函数为：

$f(\mathbf{x})=\mathbf{sgn}\left(\sum_{i=1}^m\alpha_i^*y_iK(\mathbf{x}_i,\mathbf{x})+b^*\right)$

$w=\sum_{i=1}^m\alpha_iy_i\mathbf{x}_i$

设两个集合 $S_+$ 和 $S_-$，集合内分别为正例和负例的支持向量（$\xi_i=0$），元素数量都为 $s$。约束变成 $y_if(\mathbf{x}_i)=\rho$。得到 $b^*$ 和 $\rho^*$：

$b^*=-\frac{1}{2s}\sum_{x\in S_+\cup S_-}\sum_{i=1}^m\alpha_i^*y_iK(\mathbf{x},\mathbf{x}_i)$

$\rho^*=\frac{1}{2s}\left(\sum_{x\in S_+}\sum_{i=1}^m\alpha_i^*y_iK(\mathbf{x},\mathbf{x}_i)-\sum_{x\in S_-}\sum_{i=1}^m\alpha_i^*y_iK(\mathbf{x},\mathbf{x}_i)\right)$

多类问题的 SVC

处理多类问题时，把多个类转化为若干个问题处理。

一对其余：用一类与其余类进行比较。

• 如将类1作为正例，其他组合一起作为负例，得到决策函数 $f_1(\mathbf{x})$；然后将类2作为正例，其余组合一起作为负例，得到决策函数 $f_2(\mathbf{x})$。以此类推得到 $k$ 个决策函数。
• 当对新样本 $\mathbf{x}$，带入下式得到分类：

$\arg\max_{i}f_i(\mathbf{x})$

一对一：一共得到 $k(k-1)/2$ 个决策函数 $f_{i,j}(\mathbf{x}),0\leq i<j\leq k$，表示第 $i$ 类和第 $j$ 类比较得到的决策函数。

• 当对新样本 $\mathbf{x}$，需要代入所有的 $f_{i,j}(\mathbf{x})$，统计所有类别的胜出次数，得票最多的类即为结果。

单类 SVM

单类问题并不是进行分类，而是判断新样本是否属于该类。

如判断银行业务中是否为欺诈交易时，无法提供足够多的欺诈例子用于训练，但有大量正常交易用于建模。

解决方法：Tax & Duin 法和 Schölkopf 法。

Tax & Duin 法：在输入空间或特征空间内找到一个体积最小的超球体，能够包含全部训练样本。

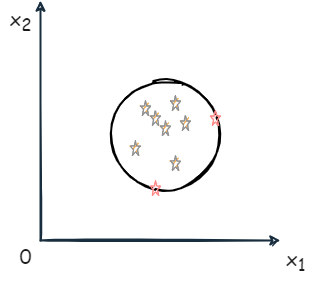
• 当然也为每个样本 $\mathbf{x}_i$ 分配一个松弛变量 $\xi_i$

带有 $\xi_i$、球心为 $\mathbf{a}$、半径为 $\mathbf{R}$ 的超球体表达式为：

$F(\mathbf{R},\mathbf{a},\xi_i)=\mathbf{R}^2+C\sum_{i=1}^m\xi_i$

• $C$ 是常数，用于平衡超球体的体积大小和超球体外样本的数量。

使得上式最小化，还需满足约束：

$\vert\vert\phi(\mathbf{x}_i)-\mathbf{a}\vert\vert^2\leq\mathbf{R}^2+\xi_i,\xi_i\geq 0, i=1,2,\ldots,m$

• $\phi(\mathbf{x}_i)$ 表示样本 $\mathbf{x}_i$ 从输入空间到特征空间的映射。

拉格朗日乘子法得到：

$L(\mathbf{R},\mathbf{a},\alpha,\xi,\mu)=\mathbf{R}^2+C\sum_{i=1}^m\xi_i-\sum_{i=1}^m\alpha_i\left[\mathbf{R}^2+\xi_i-\vert\vert\phi(\mathbf{x}_i)-\mathbf{a}\vert\vert^2\right]-\sum_{i=1}^m\mu_i\xi_i$

• $\alpha_i$ 和 $\mu_i$ 都不小于0。

基于变量 $\mathbf{R}$、$\mathbf{a}$、$\xi_i$ 的偏导数分别为：

$\sum_{i=1}^m\alpha_i=1$

$\mathbf{a}=\sum_{i=1}^m\alpha_i\phi(\mathbf{x}_i)$

$C-\alpha_i-\mu_i=0$

通过代入得到对偶公式：

$L(\mathbf{R},\mathbf{a},\alpha,\xi,\mu)=\sum_{i=1}^m\alpha_i\phi(\mathbf{x}_i)\cdot\phi(\mathbf{x}_i)-\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_j\phi(\mathbf{x}_i)\cdot\phi(\mathbf{x}_j)$

使用核函数代替点乘，得到二次优化问题：

$\max_\alpha\sum_{i=1}^m\alpha_iK(\mathbf{x}_i,\mathbf{x}_i)-\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jK(\mathbf{x}_i,\mathbf{x}_j)\\ 受限于\sum_{i=1}^m\alpha_i=1,\ 0\leq\alpha_i\leq C, i=1,2,\ldots,m$

在超球体表面的样本为支持向量。

• 超球体的半径 $\mathbf{R}$ 可通过计算球心 $\mathbf{a}$ 到任意一个支持向量的距离得到。

设解为 $\alpha^*=(\alpha_1^*,\alpha_2^*,\cdots+\alpha_m^*)$，支持向量为 $\mathbf{x}_s$ ：

$\mathbf{R}^2=\vert\vert\phi(\mathbf{x}_j)-\mathbf{a}\vert\vert\vert^2\\ =\vert\vert\phi(\mathbf{x}_s)-\sum_{i=1}^m\alpha_i^*\phi(\mathbf{x}_i)^2\vert\vert\\ =K(\mathbf{x}_s,\mathbf{x}_s)-2\sum_{i=1}^m\alpha_i^*K(\mathbf{x}_s,\mathbf{x}_s)+\sum_{i=1}^m\sum_{j=1}^m\alpha_i^*\alpha_j^*K(\mathbf{x}_i,\mathbf{x}_j)$

当判断样本是否属于该类时，需要计算样本 $\mathbf{x}$ 与球心的距离 $a$，并与半径 $\mathbf{R}$ 比较，如果小于半径，则是该类，否则不属于该类。

决策函数：

$f(x)=\mathbf{sgn}(d(\mathbf{x}))$

$\begin{aligned} f(x)&=\mathbf{sgn}\left(\mathbf{R}^2-K(\mathbf{x},\mathbf{x})+2\sum_{i=1}^m\alpha_i^*K(\mathbf{x}_i,\mathbf{x})-\sum_{i=1}^m\sum_{j=1}^m\alpha_i^*\alpha_j^*K(\mathbf{x}_i,\mathbf{x}_j)\right)\\ &=\mathbf{sgn}\left(K(\mathbf{x}_s,\mathbf{x}_s)-K(\mathbf{x},\mathbf{x})-2\sum_{i=1}^m\alpha_i^*[K(\mathbf{x}_i,\mathbf{x}_s)-K(\mathbf{x}_i,\mathbf{x})]\right) \end{aligned}$

• $\mathbf{x}_s$ 表示任意一个支持向量；
• 当 $f(\mathbf{x})=1$，表示 $\mathbf{x}$ 属于该类。

Schölkopf 法：在特征空间找到一个超平面，该超平面能够分隔全部样本和坐标原点，并且要使该超平面到远点的距离最远。

求解：

$\min\frac{1}{2}\vert\vert w\vert\vert^2+\frac{1}{\nu m}\sum_{i=1}^m\xi_i-\rho\\ 受限于\ (w\cdot\phi(\mathbf{x}_i))\geq\rho-\xi_i,\xi_i\geq 0,i=1,2,\ldots,m$

• $\nu$ 表示支持向量占全部训练样本的比例下限，也表示错误分类样本占全部训练样本的比例上限。

做拉格朗日方程：

$L(w,\xi,\rho,\alpha,\mu)=\frac{1}{2}\vert\vert w\vert\vert^2+\frac{1}{\nu m}\sum_{i=1}^m\xi_i-\rho-\sum_{i=1}^m\alpha_i(w\cdot\phi(\mathbf{x}_i)-\rho+\xi_i)-\sum_{i=1}^m\mu_i\xi_i$

对 $w、\xi、\rho$ 求偏导，使其为0，有：

$w=\sum_{i=1}^m\alpha_i\phi(\mathbf{x}_i)$

$\alpha_i=\frac{1}{\nu m}-\mu_i\Rightarrow\alpha_i\leq\frac{1}{\nu m}$

$\sum_{i=1}^m\alpha_i=1$

则对偶问题为：

$\max_{\alpha}-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_iK(\mathbf{x}_i,\mathbf{x}_j)\\ 受限于\ \sum_{i=1}^m\alpha_i=1,0\leq\alpha_i\leq\frac{1}{\nu m},i=1,2,\ldots,m$

设解为 $\alpha^*=(\alpha_1^*,\alpha_2^*,\cdots,\alpha_m^*)$，若 $\alpha_i$ 和 $\mu_i$ 都不为0，则 $\xi_i$ 必为0：

$\rho=(w\cdot\phi(\mathbf{x}_s))$

• $\mathbf{x}_s$ 为任意一个支持向量。

由 $\alpha_j$ 不为0，代入 $w=\sum_{i=1}^m\alpha_i\phi(\mathbf{x}_i)$，则：

$\rho=(w\cdot\phi(\mathbf{x}_s))=\sum_{i=1}^m\alpha_iK(\mathbf{x}_i,\mathbf{x}_s)$

决策函数：

$f(\mathbf{x})=\mathbf{sgn}(d(\mathbf{x}))=\mathbf{sgn}((w\cdot\phi(\mathbf{x}))-\rho)$

$f(\mathbf{x})=\mathbf{sgn}\left(\sum_{i=1}^m\alpha_i^*K(\mathbf{x}_i,\mathbf{x})-\sum_{i=1}^m\alpha_i^*K(\mathbf{x}_i,\mathbf{x}_s)\right)$

• $\mathbf{x}_s$ 为任意一个支持向量。
• $\mathbf{x}$ 为待预测样本。
• 当 $f(\mathbf{x})=1$，表示 $\mathbf{x}$ 属于该类。

ε-SVR 算法

Vapnik 通过 $\varepsilon$ 不敏感损失函数，把 SVM 扩展到回归问题中。

设 $y_i$ 为样本 $\mathbf{x}$ 对应的响应值，回归问题则是找到一个函数 $f(\mathbf{x})$，使得 $f(\mathbf{x}_i)=y_i$。

• 估计的质量好坏由不敏感损失函数衡量。

$\mathbf{Loss}_\varepsilon=\begin{cases}0,& 如果\vert y-f(\mathbf{x})\leq\varepsilon\\\vert y-f(\mathbf{x})\vert-\varepsilon,& 其他\end{cases}$

• $\varepsilon>0$，表示控制误差限度的常量，即如果误差在 $[-\varepsilon,\varepsilon]$ 之间，就认为忽略误差。

线性关系时，函数表示为：

$f(\mathbf{x})=w\cdot\mathbf{x}+b$

• $w$ 为权重，$b$ 为偏置。

由于误差允许，所以在 $f(\mathbf{x})$ 周围形成一个包围，称之为 $\varepsilon$ 管。

$\varepsilon$-SVR 中，得到 $f(\mathbf{x})$ 还需要满足：

1. 使 $f(\mathbf{x})$ 与测量值 $y_i$ 的偏差值不大于 $\varepsilon$，让所有样本都在 $\varepsilon$ 管中。
2. 使 $f(\mathbf{x})$ 尽可能平坦，简化模型，能够避免过拟合。平直指的是样本中各个特征属性对样本贡献大小应该均衡，即 $w$ 要小。

$\varepsilon$-SVR 问题表示为：

$\min\frac{1}{2}\vert\vert w\vert\vert^2\\ 受限于\begin{cases}y_i-w\cdot \mathbf{x}_i-b\leq\varepsilon\\ w\cdot\mathbf{x}_i+b-y_i\leq\varepsilon\end{cases},i=1,2,\ldots,m$

也使用软间隔，引入两个松弛变量 $\xi^+$ 和 $\xi^-$，上式改写为：

• $\xi_i^+$ 表示那些被高估的样本响应值的误差；
• $\xi_i^-$ 表示那些被低估的样本响应值的误差

$\min\frac{1}{2}\vert\vert w\vert\vert^2+C\sum_{i=1}^m(\xi_i^++\xi_i^-)\\ 受限于\begin{cases}y_i-w\cdot \mathbf{x}_i-b\leq\varepsilon+\xi_i^-\\ w\cdot\mathbf{x}_i+b-y_i\leq\varepsilon+\xi_i^+\end{cases},\ \begin{cases}\xi_i^-\geq 0\\\xi_i^+\geq 0\end{cases},\ i=1,2,\ldots,m$

• $C>0$：为常数，均衡 $f(\mathbf{x})$ 的平坦程度与偏差大于 $\varepsilon$ 的样本数量。

$\vert\xi\vert_\varepsilon=\begin{cases}0,& 如果\vert\xi\vert\leq\varepsilon\\\vert\xi\vert-\varepsilon,& 其他\end{cases}$

表示改写后的拉格朗日乘子法方程为：

$L(w,b,\xi,\alpha,\mu)=\frac{1}{2}\vert\vert w\vert\vert^2+C\sum_{i=1}^m(\xi_i^++\xi_i^-)-\sum_{i=1}^m(\mu_i^+\xi_i^++\mu_i^-\xi_i^-)\\ -\sum_{i=1}^m\alpha_i^+(\varepsilon+\xi_i^++y_i-w\cdot\mathbf{x}_i-b)-\sum_{i=1}^m\alpha_i^-(\varepsilon+\xi_i^--y_i+w\cdot\mathbf{x}_i+b)$

• $\alpha_i^+、\alpha_i^-、\mu_i^+、\mu_i^-$ 都为非负值。

对原变量 $w、b、\xi$ 进行求偏导并使其为0：

$\frac{\partial L}{\partial w}=w-\sum_{i=1}^m(\alpha_i^--\alpha_i^+)\mathbf{x}_i=0\Rightarrow w=\sum_{i=1}^m(\alpha_i^--\alpha_i^+)\mathbf{x}_i$

$\frac{\partial L}{\partial b}=\sum_{i=1}^m(\alpha_i^+-\alpha_i^-)=0$

$\frac{\partial L}{\partial \xi^+}=C-\mu_i^+-\alpha_i^+=0$

$\frac{\partial L}{\partial \xi^-}=C-\mu_i^--\alpha_i^-=0$

进入代入，得到对偶优化问题：

$\max_{\alpha^-,\alpha^+}-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m(\alpha_i^--\alpha_i^+)(\alpha_j^--\alpha_j^+)K(\mathbf{x}_i,\mathbf{x}_j)-\varepsilon\sum_{i=1}^m(\alpha_i^-+\alpha_i^+)+\sum_{i=1}^my_i(\alpha_i^--\alpha_i^+)\\ 受限于\ \sum_{i=1}^m(\alpha_i^--\alpha_i^+)=0,\ \alpha_i^-,\alpha_j^+\in[0,C]$

• $K(\mathbf{x}_i,\mathbf{x}_j)$：为核函数，同前映射关系。

设解为 $\alpha^*=(\alpha_1^{-*},\alpha_1^{+*},\cdots,\alpha_m^{-*},\alpha_m^{+*})$，则：

$w=\sum_{i=1}^m(\alpha_i^{-*}-\alpha_i^{+*})\phi(\mathbf{x}_i)$

最后回归计算公式：

$f(\mathbf{x})=\sum_{i=1}^m(\alpha_i^{-*}-\alpha_i^{+*})K(\mathbf{x}_i,\mathbf{x})+b^*$

由 KKT 条件计算：

$b^*=y_j-\sum_{i=1}^m(\alpha_i^{-*}-\alpha_i^{+*})K(\mathbf{x}_i,\mathbf{x}_j)+\varepsilon$

或

$b^*=y_k-\sum_{i=1}^m(\alpha_i^{-*}-\alpha_i^{+*})K(\mathbf{x}_i,\mathbf{x}_k)-\varepsilon$

• $(\mathbf{x}_j,y_j)$ 为任意一个样本对应的 $\alpha_j^{+*}\in(0,C)$；
• $(\mathbf{x}_k,y_k)$ 为任意一个样本对应的 $\alpha_k^{-*}\in(0,C)$。

由 KKT 条件，还可以知道 $\alpha_i^{-*}$ 或 $\alpha_i^{+*}$ 等于 $C$ 的样本在 $\varepsilon$ 管外，而且 $\alpha_i^{-*}$ 或 $\alpha_i^{+*}$ 不可能同时为0。

这意味着一个样本不能拥有两个方向的松弛变量 $\xi$，只能向一个方向偏离。

ν-SVR 算法

Schölkopf 从 ν-SVC 算法上扩展得到 ν-SVR 算法。

ν-SVR 原公式：

$\min\frac{1}{2}\vert\vert w\vert\vert^2+C\left(\nu\varepsilon+\frac{1}{m}\sum_{i=1}^m(\xi_i^++\xi_i^-)\right)\\ 受限于\ \begin{cases}y_i-w\cdot\phi(\mathbf{x}_i)-b\leq\varepsilon+\xi_i^-\\ w\cdot\phi(\mathbf{x}_i)+b-y_i\leq\varepsilon+\xi_i^+\end{cases},\ \begin{cases}\xi_i^-\geq 0\\\xi_i^+\geq 0\end{cases},\ i=1,2,\ldots,m$

$\varepsilon$-SVR 中，参数 $\varepsilon$ 通过经验选取，而在 $\nu$-SVR 中把 $\varepsilon$ 作为目标函数的一个变量。同时 $C$ 和 $\nu$ 为常数， $C$ 为正值； $\nu\in[0,1]$ 同样表示支持向量占全部训练样本的比例下限，也表示错误估计样本占全部训练样本的比例上限。

取拉格朗日方程为：

$L(w,b,\beta,\varepsilon,\xi,\alpha,\mu)=\frac{1}{2}+C\nu\varepsilon+\frac{C}{m}\sum_{i=1}^m(\xi_i^++\xi_i^-)-\beta\varepsilon-\sum_{i=1}^m(\mu_i^+\xi_i^++\mu_i^-\xi_i^-)\\ -\sum_{i=1}^m\alpha_i^+(\varepsilon+\xi_i^++y_i-w\cdot\phi(\mathbf{x}_i)-b)-\sum_{i=1}^m\alpha_i^-(\varepsilon+\xi_i^--y_i+w\cdot\phi(\mathbf{x}_i)+b)$

对原变量 $w、\varepsilon、b、\xi$ 求偏导并使之为0：

$\frac{\partial L}{\partial w}=w-\sum_{i=1}^m(\alpha_i^--\alpha_i^+)\phi(\mathbf{x}_i)=0\Rightarrow w=\sum_{i=1}^m(\alpha_i^--\alpha_i^+)\phi(\mathbf{x}_i)$

$\frac{\partial L}{\partial \varepsilon}=C\nu-\sum_{i=1}^m(\alpha_i^++\alpha_i^-)-\beta=0$