机器学习基础入门：神经网络

神经网络是一种模仿生物神经系统的机器学习算法。

神经元

人工神经网络由若干个神经元构成。神经元结构如下：

神经元

$x_1、x_2、...、x_n$ 是神经元的输入。
$y$ 是神经元的输出。
$w_1、w_2、...、w_n$ 是神经元的权重。
$b$ 为偏移量。

神经元内部包括两个部分：

输入的加权求和；

u=\sum_{i=1}^n(w_ix_i)+b=\sum_{i=0}^n(w_ix_i),x_0恒为1

对求和结果的“激活”。激活指的是对输出值进行某种关系映射，使得神经元兴奋或抑制。

y=f(u)

激活函数有多种：

线性函数：

f(x)=x

阈值函数：

f(x)=\begin{cases}1,&x\geq\theta\\0,&x<\theta\end{cases}

Sigmoid 函数：

f(x)=\frac{1}{1+e^{-x}}

对称 Sigmoid 函数：

f(x)=\beta\frac{1-e^{-\alpha x}}{1+e^{-\alpha x}}

双曲正切函数：

f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}

高斯函数：

f(x)=\beta e^{-\alpha^2x^2}

RELU 函数：

f(x)=\max(0,x)

感知器

感知器由两层神经元组成：

输入层：输入数据
输出层：处理并输出结果

感知器的学习规则很简单，对于训练样本 $(\mathbf{x},y)$ ，若当前感知机输出为 $\hat{y}$ ，则权重调整为：

w_i=w_i+\Delta w_i=w_i\eta(y-\hat{y})x_i

$\eta\in(0,1)$ 称为学习率。

感知器只有输出层神经元进行激活函数处理，也就是只有一层功能神经元，处理线性可分问题。

存在一个线性超平面将样本分开，则感知器的学习过程会收敛。

多层感知器 MLP

解决非线性可分问题，需要考虑多层（功能）神经元。

前馈神经网络是神经网络的一种，包括一个输入层、一个输出层和若干个隐含层。

某一层的神经元只能通过一个方向连接到下一层的神经元。

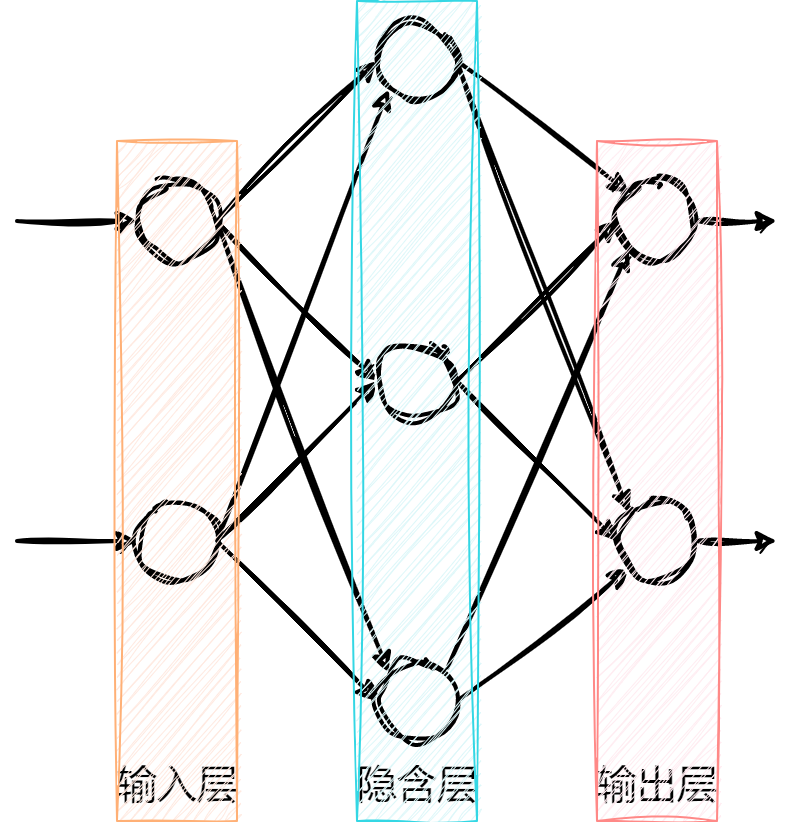
前馈神经网络

像上图这种拓扑结构的神经网络又称为多层感知器（MLP，Multi-Layer Perceptron）。

MLP 可以用 Backprop（backward propagation of errors，误差反向传播，BP）算法实现建模。

BP 算法输入层的神经元数量一般为样本的特征属性数量，输出层的神经元的数量一般为样本的所有可能目标值的数量。

对于分类问题，输出层的神经元数量为分类数量。

BP 算法的核心思想是：通过前向通路得到误差，再把误差反向传播，实现权值的修正。

MPL 的误差可以用平方误差函数表示。

设某个样本 $\mathbf{x}=(x_1,x_2,...,x_n)$ 对应的目标值为 $t$ ，有 $J$ 种可能值， $t=\{t_1,t_2,...,t_j\}$ 。
则 MLP 输入层一共有 $n$ 个神经元，输出层（第 $L$ 层）有 $J$ 个神经元。

设样本 $\mathbf{x}$ 经过前向通路得到的最终输出为 $y=\{y_1^L,y_2^L,...,y_j^L\}$ 。

下标表示神经元的索引，上标表示所在的层

则该样本的平方误差为：

E=\frac{1}{2}\sum_{j=1}^J(t_j-y_j^L)^2

$\frac{1}{2}$ 为方便求导系数，不影响误差的变化趋势。

MLP 的目标是使得 $E$ 最小。通过改变权值 $w$ ，从而使得 $E$ 最小。

Backprop算法是一种迭代的方法，渐进地减小 $E$ 。

梯度下降法

误差 $E$ 对权值 $w$ 的导数为 $w$ 的变化率：

\Delta w=-\eta\frac{dE}{dw}

$\eta\in(0,1)$ $η \in (0, 1)$ 表示学习效率，控制收敛速度和准确性。
- $\eta$ 过大，导致震荡，很难收敛；
- $\eta$ 过小，导致长时间不能收敛。

引入“动量” $\mu$ ，改变因 $\eta$ 的选取不好而带来的问题，上式改写为：

\Delta w(t)=-\eta\frac{dE}{dw}(t)+\mu\Delta w(t-1)

$t$ 表示当前， $t-1$ 表示上一次， $t+1$ 表示下一次。
说明本次的 $w$ 变化率不仅与 $E$ 的导数相关，还与上一次 $w$ 的变化率相关。
$\mu$ 提供了一些惯性，使之平滑权值的随机波动。

由 $\Delta w$ 更新当前权值 $w$ ：

w(t+1)=w(t)+\Delta w(t)

上式表示了更新权值的过程是从输出层到隐含层，向输入层逐层推进的过程，即误差的反向传播。

当所有权值更新完后，再由前向通路计算得到新的误差 $E$ ，完成一次迭代。

具体计算过程

设 $w_{kh}^l$ 表示第 $l$ 层的第 $k$ 个神经元与第 $l-1$ 层的第 $h$ 和神经元之间连接的权值。第 $l$ 层的第 $k$ 个神经元的输出 $y_k^l$ 为：

y_k^l=f(u_k^l)=f\left(\sum_{h=1}^H(w_{kh}^ly_h^{l-1})+b_k^l\right)

$u_k^l$ 表示第 $l$ 层第 $k$ 个神经元的加权和；
$b_k^l$ 表示第 $l$ 层第 $k$ 个神经元的偏置。

若第 $l$ 层共有 $K$ 个神经元，第 $l-1$ 层共有 $H$ 个神经元，则第 $l$ 层的 $K$ 个神经元的加权和 $u^l$ 可以用矩阵表示：

u^l=\left(\begin{matrix}u_1^l\\u_2^l\\\vdots\\u_K^l\end{matrix}\right)=\left(\begin{matrix}w_{11}^l&w_{12}^l&\cdots&w_{1H}^l\\w_{21}^l&w_{22}^l&\cdots&w_{2H}^l\\\vdots&\vdots&\ddots&\vdots\\w_{K1}^l&w_{K2}^l&\cdots&w_{KH}^l\end{matrix}\right)\left(\begin{matrix}y_1^{l-1}\\y_2^{l-1}\\\vdots\\y_H^{l-1}\end{matrix}\right)+\left(\begin{matrix}b_1^l\\b_2^l\\\vdots\\b_K^l\end{matrix}\right)

第 $l$ 层的所有 $K$ 个神经元输出 $y^l$ 为：

y^l=\left(\begin{matrix}y_1^l\\y_2^l\\\vdots\\y_K^l\end{matrix}\right)=\left(\begin{matrix}f(u_1^l)\\f(u_2^l)\\\vdots\\f(u_K^l)\end{matrix}\right)=f(u^l)

把每层的输出 $y^l$ 级联在一起，就构成了 MLP 的前向通路。

当一个样本添加到输入层时，通过层层计算得到最终输出 $y^L$ ，再代入误差计算中得到误差。

前向通路过程为，样本进行权值计算，通过激活输出，最后得到误差：

w_{kh}^l\rightarrow u_k^l\rightarrow y_k^l\rightarrow E

计算权值变化率，即对误差求导，由链式法则可知，样本 $\mathbf{x}$ 的误差 $E$ 对权值 $w_{kh}^l$ 的偏导数为：

\frac{\partial E}{\partial w_{kh}^l}=\frac{\partial E}{\partial y_k^l}\frac{\partial y_k^l}{\partial u_k^l}\frac{\partial u_k^l}{\partial w_{kh}^l}

定义 $\delta_k^l$ 为上式等号右侧的前两项偏导， $\delta_k^l=\frac{\partial E}{\partial y_k^l}\frac{\partial y_k^l}{\partial u_k^l}=\frac{\partial E}{\partial u_k^l}$

计算上式等号右侧第三个偏导，有：

\frac{\partial u_k^l}{\partial w_{kh}^l}=\frac{\partial}{\partial w_{kh}^l}\left[\sum_{h=1}^H(w_{kh}^ly_h^{l-1})+b_k^l\right]\\ \frac{\partial u_k^l}{\partial w_{kh}^l}=\frac{\partial}{\partial w_{kh}^l}\left(w_{k1}^ly_1^{l-1}+\cdots+w_{kh}^ly_h^{l-1}+\cdots+w_{kH}^ly_H^{l-1}+b_k^l\right)\\ \frac{\partial u_k^l}{\partial w_{kh}^l}=y_h^{l-1}

求导的结果为第 $l-1$ 层的第 $h$ 个神经元的输出。如果第 $l-1$ 为输入层，则 $y_h^{l-1}$ 为样本的第 $h$ 个属性。

计算上式等号右侧第二个偏导，有：

\frac{\partial y_k^l}{\partial u_k^l}=\frac{\partial f(u_k^l)}{\partial u_k^l}=f'(u_k^l)

$f(\cdot)$ 表示激活函数。
线性函数求导为： $\frac{df(x)}{dx}=\frac{d}{dx}x=1$ 。
Sigmoid 函数求导为： $\frac{df(x)}{dx}=\frac{d}{dx}\left(\frac{1}{1+e^{-x}}\right)=\frac{1}{1+e^{-x}}\left(1-\frac{1}{1+e^{-x}}\right)=f(x)(1-f(x))$
对称 Sigmoid 函数求导为： $\frac{df(x)}{dx}=\frac{d}{dx}\left(\beta\frac{1-e^{-\alpha x}}{1+e^{-\alpha x}}\right)=2\alpha\beta\frac{e^{-\alpha x}}{(1+e^{-\alpha x})^2}$
双曲正切函数求导为： $\frac{df(x)}{dx}=\frac{d}{dx}\left(\frac{e^x-e^{-x}}{e^x+e^{-x}}\right)=1-f^2(x)$
高斯函数求导为： $\frac{df(x)}{dx}=\frac{d}{dx}\left(\beta e^{-\alpha^2x^2}\right)=-2\alpha^2\beta xe^{-\alpha^2x^2}$

计算上式等号右侧第一个偏导，当 $y_k^l$ 为输出层的输出时，即 $y_j^L$ ，有：

\frac{\partial E}{\partial y_j^L}=\frac{\partial}{\partial y_j^L}\left[\frac{1}{2}\sum_{j=1}^J(t_j-y_j^L)^2\right]\\ \frac{\partial E}{\partial y_j^L}=\frac{\partial}{\partial y_j^L}\left[\frac{1}{2}(t_1-y_1^L)^2+\cdots+\frac{1}{2}(t_j-y_j^L)^2+\cdots+\frac{1}{2}(t_J-y_J^L)^2\right]\\ \frac{\partial E}{\partial y_j^L}=y_j^L-t_j

所以，基于输出层的权值 $y_{jh}^L$ 误差导数为：

\frac{\partial E}{\partial w_{jh}^L}=(y_j^L-t_j)f'(u_j^L)y_h^{L-1}

$\delta_j^L=(y_j^L-t_j)f'(u_j^L)$

不知道内部神经元的输出误差，只知道输出层的误差，所以需要把内部神经元误差传递到输出层。

又因为神经元都直接或间接地相互连接，所以内部所有神经元的误差最终都会传递到输出层的所有神经元上。

设 $y_h^l$ 为中间第 $l$ 层的第 $h$ 个神经元的输出，则：

\frac{\partial E}{\partial y_h^l}=\frac{\partial}{\partial y_h^l}\left[E(u_1^{l+1}),\cdots,E(u_K^{l+1})\right]

$E(u_k^{l+1})$ 表示误差 $E$ 是关于 $u_k^{l+1}$ 的函数。

上式表明，第 $l$ 层的第 $h$ 个神经元的输出误差传递到第 $l+1$ 层内的所有 $K$ 个神经元内，则：

\frac{\partial E}{\partial y_h^l}=\sum_{k=1}^K\left(\frac{\partial E}{\partial u_k^{l+1}}\frac{\partial u_k^{l+1}}{\partial y_h^l}\right)

计算右侧第二个偏导：

\frac{\partial u_k^{l+1}}{\partial y_h^l}=\frac{\partial}{\partial y_h^l}\left[\sum_{h=1}^H(w_{kh}^{l+1}y_h^l)+b_k^{l+1}\right]\\ \frac{\partial u_k^{l+1}}{\partial y_h^l}=\frac{\partial}{\partial y_h^l}(w_{k1}^{l+1}y_1^l+\cdots+w_{kh}^{l+1}y_h^l+\cdots+w_{kH}^{l+1}y_H^l+b_k^{l+1})\\ \frac{\partial u_k^{l+1}}{\partial y_h^l}=w_{kh}^{l+1}

计算右侧第一个偏导：

\frac{\partial E}{\partial u_k^{l+1}}=\delta_k^{l+1}

所以，基于中间层的权值 $w_{kh}^l$ 的误差导数为：

\frac{\partial E_p}{\partial w_{kh}^l}=\left[\sum_{k=1}^K(w_{kh}^{l+1}\delta_k^{l+1})\right]f'(u_k^l)y_h^{l-1}

先得到输出层的结果，再计算倒数第二层，以此类推，完整的误差导数：

\frac{\partial E}{\partial w_{kh}^l}=\delta_k^ly_h^{l-1},其中\delta_k^l=\begin{cases}(y_k^l-t_k)f'(u_k^l),&l为输出层\\\left[\sum_{k=1}^K(w_{kh}^{l+1}\delta_k^{l+1})\right]f'(u_k^l),&l为中间层\end{cases}

把上式的结果代入计算得到 权值的变化率。再由 $w(t+1)=w(t)+\Delta w(t)$ 得到更新后的权值。经过新权值计算下一样本，反复进行。

计算的方法：

在线方法：样本一个一个地进入 MLP，每完成一个样本的计算，就更新一次权值。
- 为了增加鲁棒性，每次迭代之前，可以把全体样本打乱顺序，这样在每次迭代的过程中，提取样本的顺序就会不相同。
批量方法：把所有样本的误差累加在一起，用该累加误差计算误差的导数，进而得到权值的变化率。

初始化权值

一般会随机选择很小的值作为初始权值。

但收敛较慢。

采用 Nguyen-Widrow 算法初始化权值：

每个神经元都有属于自己的一个区间范围，通过初始化权值就可以限制它的区间位置。当改变权值时，也在自己的区间范围内变化。

Nguyen-Widrow 算法初始化 MLP 权值的方法为：

对于所有连接输出层的权值和偏移量，初始值为在 $-1$ 到 $1$ 之间的随机数；
对于中间层的权值，初始化为（ $\nu_h$ 为 $-1$ 到 $1$ 之间的随机数， $H$ 为第 $l-1$ 层神经元的数量）：

w_{kh}^l=\frac{\nu_h}{\sum_{h=1}^H\vert\nu_h\vert}

对于中间层的偏移量，初始化为（ $\nu_k$ 为 $-1$ 到 $1$ 之间的随机数， $K$ 为第 $l$ 层神经元的数量）：

b_k^l=\left(\frac{2k}{K}-1\right)\nu_kG

G=0.7H^{\frac{1}{K-1}}

RPROP

上述 BP 算法的权值变化基于误差梯度的变化率。

而 RPROP 算法的权值变化基于它的符号：

\Delta w(t)=\begin{cases}-\Delta(t),&\frac{\partial E}{\partial w}(t)>0\\+\Delta(t),&\frac{\partial E}{\partial w}(t)<0\\0,&其他\end{cases}

其中，

\Delta(t)=\begin{cases}\eta^+\Delta(t-1),&\frac{\partial E}{\partial w}(t-1)\frac{\partial E}{\partial w}(t)>0\\\eta^-\Delta(t-1),&\frac{\partial E}{\partial w}(t-1)\frac{\partial E}{\partial w}(t)<0\\\Delta(t-1),&其他\end{cases}

常数 $\eta^+$ 必须大于1；
常数 $\eta^-$ 必须在0~1之间。
$\partial E/\partial w$ 由下式得到：

\frac{\partial E}{\partial w_{kh}^l}=\delta_k^ly_h^{l-1},其中\delta_k^l=\begin{cases}(y_k^l-t_k)f'(u_k^l),&l为输出层\\\left[\sum_{k=1}^K(w_{kh}^{l+1}\delta_k^{l+1})\right]f'(u_k^l),&l为中间层\end{cases}

$\Delta(0)=0.1$ 比较好；
$\Delta_{max}(t)=50,\Delta_{min}(t)=10^{-6}$ 可以防止溢出。

OpenCV 提供的 ANN

OpenCV 提供的神经网络算法有：

enum TrainingMethods
{
    BACKPROP=0,     // BP 算法
    RPROP = 1,      // RPROP 算法
    ANNEAL = 2      // 模拟退火算法
};

通过函数设置：

// param1：
//      - 对于RPROP算法，传递给setRpropDW0；
//      - 对于BP算法，传递给setBackpropWeightScale；
//      - 对于模拟退火算法，传递给initialT。
// param2：
//      - 对于RPROP算法，传递给setRpropDWMin；
//      - 对于BP算法，传递给setBackpropMomentumScale；
//      - 对于模拟退火算法，传递给finalT。
void setTrainMethod(int method, double param1 = 0, double param2 = 0);

int getTrainMethod();

OpenCV 提供的激活函数（目前，默认和唯一完全支持的激活函数是对称 Sigmoid）：

enum ActivationFunctions
{
    // 线性函数
    IDENTITY = 0,
    
    // 对称 Sigmoid 函数
    SIGMOID_SYM = 1,

    // 高斯函数
    GAUSSIAN = 2,
    
    // ReLU 函数：f(x)=max(0,x)
    RELU = 3,

    // Leaky ReLU 函数：当 x>0，f(x)=x；当 x<=0，f(x)=αx
    LEAKYRELU= 4
};

通过函数设置：

1
2
3

// param1：激活函数的第一个参数，α
// param2：激活函数的第二个参数，β
void setActivationFunction(int type, double param1 = 0, double param2 = 0);

部分参数如下：

LayerSizes：指定每层神经元的数量，包括输入和输出层。参数为向量，第一个元素指定了输入层中元素的数量。最后一个元素为输出层中元素的数量。默认值为空。

1 2	void setLayerSizes(InputArray _layer_sizes); cv::Mat getLayerSizes() const = 0;

BackpropWeightScale：权重梯度项的强度，
推荐值为0.1左右，默认值为0.1。

1 2	double getBackpropWeightScale(); void setBackpropWeightScale(double val);

BackpropMomentumScale：动量项的强度，该参数提供了一些惯量来平滑权重的随机波动。默认值为0.1。

1 2	double getBackpropMomentumScale(); void setBackpropMomentumScale(double val);

propDW0：RPROP 中的 $\Delta_0$ ，默认值为0.1。

1 2	double getRpropDW0(); void setRpropDW0(double val);

RpropDWPlus：RPROP 中的增加因子 $\eta^+$ ，默认值为1.2。

1 2	double getRpropDWPlus(); void setRpropDWPlus(double val);

RpropDWMinus：RPROP 中的减少因子 $\eta^-$ ，默认值为0.5。

1 2	double getRpropDWMinus(); void setRpropDWMinus(double val);

RpropDWMin 和 RpropDWMax：RPROP 中的 $\Delta_{min}(t)$ 和 $\Delta_{max}(t)$

// Default value is FLT_EPSILON.
double getRpropDWMin();
void setRpropDWMin(double val);

// Default value is 50.
double getRpropDWMax();
void setRpropDWMax(double val);

模拟退火相关：

// 更新初始温度，默认值为 10
double getAnnealInitialT();
 void setAnnealInitialT(double val);

// 更新最终温度，默认值为 0.1
double getAnnealFinalT();
void setAnnealFinalT(double val);

// 更新冷却比，默认值为 0.95
double getAnnealCoolingRatio();
void setAnnealCoolingRatio(double val);

// 每一步更新迭代，默认值为 10
int getAnnealItePerStep();
void setAnnealItePerStep(int val);

// 设置/初始化退火RNG
void setAnnealEnergyRNG(const RNG& rng);

TermCriteria：迭代条件。

例子-糖尿病预测（MLP）

数据集在贝叶斯分类器学习记录中使用过，详见贝叶斯分类器。

数据集属性如下：

Pregnancies: 怀孕次数
Glucose：血浆葡萄糖浓度
BloodPressure：舒张压
SkinThickness：肱三头肌皮肤褶皱厚度
Insulin：两小时胰岛素含量
BMI：身体质量指数，即体重除以身高的平方
DiabetesPedigreeFunction：糖尿病血统指数，即家族遗传指数
Age：年龄

使用 MLP 进行预测结果与贝叶斯分类器比较如下：

Train Data imported: 668
Test Data imported: 100
正态贝叶斯分类器：
计算花费时长：0ms
正确率：0.76

Train Data imported: 668
Test Data imported: 100
神经网络（BP）算法(基于OpenCV实现)：
计算花费时长：230ms
正确率：0.82

代码地址：Gitee - ANN_MLP