基础线性模型

基本形式

对于一个样本 $\pmb{x}=(x_1,x_2,...,x_d)$，其中 $x_i$ 为第 $i$ 个属性上的取值。

线性模型试图通过一个属性值与权值的线性组合进行预测：

$f(x)=\omega_1x_1+\omega_2x_2+...+\omega_dx_d+b$

向量模式写成：

$f(\pmb{x})=\pmb{\omega}^T\pmb{x}+b\\ \pmb{\omega}=(\omega_1,\omega_2,...,\omega_d)$

线性回归

一元线性回归

线性回归对于样本 $(x_i,y_i)$ ，试图使：

$f(x_i)=\omega x_i+b近似于y_i$

通过均方误差评估 $f(x_i)$ 与 $y_i$ 之间的差别，试图让均方误差取最小值：

$(w^*,b^*)=\arg\min_{(w,b)} \sum_{i=1}^m(f(x_i)-y_i)^2=\arg\min_{(w,b)} \sum_{i=1}^m(y_i-f(x_i))^2\\ (w^*,b^*)=\arg\min_{(w,b)} \sum_{i=1}^m(y_i-wx_i-b)^2$

• $(\omega^*,b^*)$ 为 $\omega$ 和 $b$ 的解，此处 $m$ 为样本数。
• $\arg\min$ 表示右式取最小值时 $\omega$ 和 $b$ 的值。
• 求均方误差也对应了求欧氏距离。

基于均方误差最小值来进行模型求解，称为最小二乘法。

• 线性回归中，最小二乘法就是试图找到一条直线，使得样本到直线上的欧式距离之和最小。

令：

$E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2$

上式分别对 $\omega$ 和 $b$ 求导：

$\frac{\partial E_{(\omega,b)}}{\partial\omega}=2(\omega\sum_{i=1}^mx_i^2-\sum_{i=1}^m(y_i-b)x_i),\\ \frac{\partial E_{(\omega,b)}}{\partial b}=2(mb-\sum_{i=1}^m(y_i-wx_i))$

使导数为0，得到：

$\omega=\frac{\sum_{i=1}^my_i(x_i-\overline{x})}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2}\\ \ \\ b=\frac{1}{m}\sum_{i=1}^m(y_i-\omega x_i)$

• $\overline{x}$ 为 $x$ 的均值。

例子-一元线性回归

对于一个一元线性回归数据集进行回归计算，效果如下：

该例子相关的数据集以及代码已置于仓库：Gitee

多元线性回归

用梯度下降求解多元线性回归。

• 梯度下降法的基本思想可以类⽐为⼀个下⼭的过程。
  • 最快的下山方式就是找到当前位置最陡峭的⽅向，然后沿着此方向向下⾛，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的⽅向，就能让函数值下降的最快。
  • 反复求取梯度，最后就能到达局部的最⼩值。

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率；

在多变量函数中，梯度是⼀个向量（向量有方向），梯度的方向就指出了函数在给定点的上升最快的方向。

梯度下降公式为：

$x^{i+1}=x^i-\alpha\frac{\partial}{\partial x_i}f(x^i)$

• $\alpha$ 称作学习率或者步长，意味着每一步走的距离。距离太大容易错过最低点，距离太小迟迟未到最低点。

如：

• 单变量函数梯度下降： $f(x)=x^2$
  • 微分为：$f'(x)=2x$
  • 初始化起点为： $x^0=1$，学习率取0.4
  • 梯度下降迭代：
    • $x^1=x^0-0.4\times 2x^0=1-0.4\times 2=0.2$
    • $x^2=x^1-0.4\times 2x^1=0.2-0.4\times 0.4=0.04$
    • $x^3=x^2-0.4\times 2x^2=0.04-0.4\times 0.08=0.008$
    • $x^4=x^3-0.4\times 2x^3=0.008-0.4\times 0.016=0.0016$
• 多变量函数的梯度下降： $f(x)=x_1^2+x_2^2$
  • 微分为：$f'(x)=2x_1+2x_2$
  • 初始化起点为： $x^0=(1,3)$，学习率取0.1
  • 梯度下降迭代：
    • $x^1=x^0-0.1\times f'(x^0)=(1,3)-0.1\times (2,6)=(0.8,2.4)$
    • $x^2=x^1-0.1\times f'(x^1)=(0.8,2.4)-0.1\times (1.6,4.8)=(0.64,1.92)$
    • $x^3=x^2-0.1\times f'(x^2)=(0.64,1.92)-0.1\times (1.28,3.84)=(0.512,1.536)$
    • ……
    • $x^{100}=(1.6296e^{-10},4.8889e^{-10})$

引入损失函数，度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。线性回归中假设模型函数为： $f(x_1,...,x_n)=w_0+w_1x_1+w_2x_2+...+w_nx_n$

• $w_i$ 为模型参数，$b$ 为偏置。
• 简化：增加特征 $x_0=1$，可以简化为：$f(x_0,...,x_n)=\sum_{i=0}^nw_ix_i$

在线性回归中，损失函数通常为样本输出和假设函数的差取平方（或者带系数）。比如对于 $m$ 个样本 $(\pmb{x_i},y_i)(i = 1, 2, ...m)$，采⽤线性回归，假设损失函数为：

$Loss(w_0,w_1,...,w_n)=\frac{1}{2m}\sum_{j=0}^m(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)^2$

• $x_i^{(j)}$：上标 $j$ 表示第 $j$ 个样本，下标 $i$ 表示第 $i$ 个特征。
• 系数 $\frac {1}{2}$ 是方便微分化简。
• $x_0^{(j)}$ 都为1。

对于上述损失函数的梯度为：

$\frac{\partial}{\partial w_i}Loss(w_0,w_1,...,w_n)=\frac{1}{m}\sum_{j=0}^m(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

接着变化：

$w_i=w_i-α\frac{1}{m}\sum_{j=0}^m(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

梯度算法变种

1. 全梯度下降算法（Full Gradient Descent）
   • 更新参数时使⽤所有的样本来进⾏更新。

$w_i=w_i-α\sum_{j=0}^m(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

2. 随机梯度下降算法（Stochastic Gradient Descent）
   • 每次只代⼊计算⼀个样本⽬标函数的梯度来更新权重，再取下⼀个样本重复此过程，直到损失函数值停⽌下降或损失函数值⼩于某个可以容忍的阈值。

$w_i=w_i-α(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

3. 小批量梯度下降算法（Mini-batch Gradient Descent）
   • 每次从训练样本集上随机抽取⼀个⼩样本集，在抽出来的⼩样本集上采⽤FG迭代更新权重。

$w_i=w_i-α\sum_{j=t}^{t+x-1}(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

4. 随机平均梯度下降算法（Stochastic Average Gradient Descent）
   • 在内存中为每⼀个样本都维护⼀个旧的梯度，随机选择第i个样本来更新此样本的梯度，其他样本的梯度保持不变，然后求得所有梯度的平均值，进⽽更新了参数。
   • m 个样本

$w_i=w_i-\frac{α}{m}(f(x_0^{(j)},x_1^{(j)},...,x_n^{(j)})-y_j)x_i^{(j)}$

例子-波士顿房价

数据集地址：https://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data

• 直接复制到本地即可，保存为 .txt 文件。

数据集具有14列：

• CRIM：城镇人均犯罪率。
• ZN：占地面积超过25,000平方英尺的住宅用地比例。
• INDUS：每个城镇非零售业务的比例。
• CHAS：Charles River虚拟变量（如果是河道，则为1;否则为0）。
• NOX：一氧化氮浓度（每千万份）。
• RM：每间住宅的平均房间数。
• AGE：1940年以前建造的自住单位比例。
• DIS：波士顿的五个就业中心加权距离。
• RAD：径向高速公路的可达性指数。
• TAX：每10,000美元的全额物业税率。
• PTRATIO：城镇的学生与教师比例。
• B：$1000(Bk - 0.63)^2$ 其中Bk是城镇黑人的比例。
• LSTAT：人口状况下降%。
• MEDV：自有住房的中位数报价, 单位1000美元。
• 前13列为属性值（即 $x_i$），第14列为房价（即 $y$）。

使用 SAG 算法进行线性回归计算。

测试结果：

1
2
3

Data imported: 506
平均误差：4.57072
迭代时长：46.329s

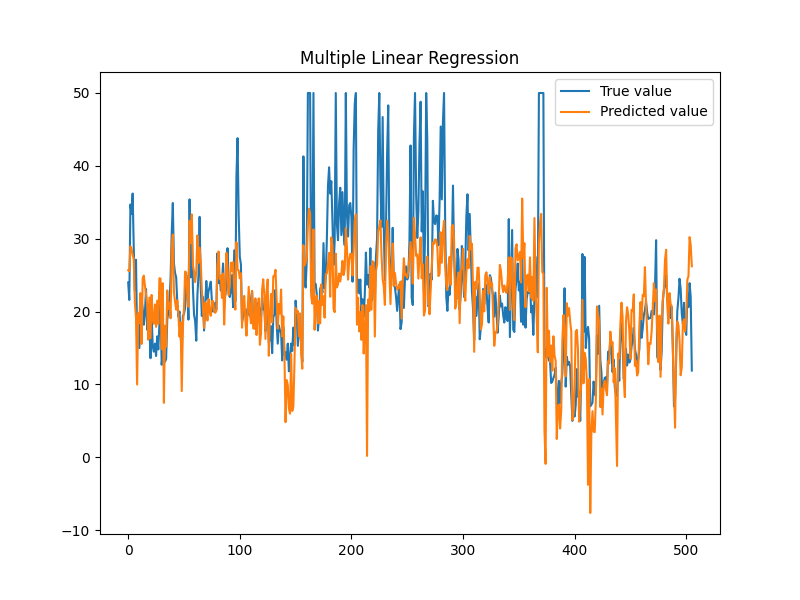
该例子相关的数据集以及代码已置于仓库：Gitee