决策树

基本流程

决策树是一种非参数的监督学习方法，可用于分类和回归。

• 构造一种模型，从样本数据的特征属性中，通过决策规则，从而预测目标变量的值。

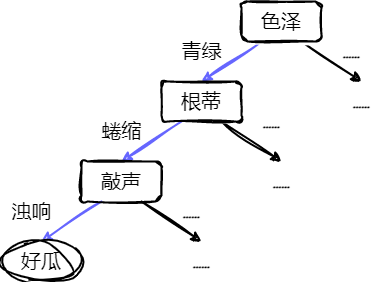
一颗决策树包含一个根结点、若干个内部结点和若干个叶结点。

• 叶结点：对应于决策结果。
• 其他每个结点对应一个属性测试。
• 根结点的范围为样本全集。
• 从根节点到每个叶结点的路径对应了一个判定测试序列。

决策树往往是自上而下，每迭代循环一次，就会选择一个特征进行分叉，直至不能再分。

• 使用“非纯度”的概念，尽量选择最佳的属性进行分叉。
  • 如果一个数据集只有一种分类结果，则该集合很“纯”。

常用有熵、基尼指数和分类误差等指标定量度量：

$熵\mathbf{Entropy}=\mathbf{E}(D)=-\sum_{j=1}^Jp_j\log_2(p_j)$

$基尼指数\mathbf{Gini}=\mathbf{Gini}(D)=\sum_{j=1}^Jp_j(1-p_j)=1-\sum_{j=1}^Jp_j^2=1-\frac{\sum_{j=1}^JN_j^2}{N^2}$

$分类误差\mathbf{Error}=1-\max{(p_j)}$

• 上三式都是值越大，表示越不纯。
• $D$ 表示样本数据的分类集合。
• 设集合有 $J$ 种分类，$p_j$ 表示第 $j$ 种分类的样本率：$p_j=\frac{N_j}{N}$
• $N$ 表示集合 $D$ 中样本数据总数，$N_j$ 表示第 $j$ 种分类的样本数。

常用的决策树算法包括第三代迭代二叉树（ID3）、C4.5、分类和回归树（CART）。

• 前两种算法是基于熵的方法。
• CART：是基于基尼指数的方法。

ID3

易知小型决策树优于大型决策树，希望分类以后降低熵的大小。使用信息增益衡量分类后熵变小的判断：

$\mathbf{G}(D,A)=\mathbf{E}(D)-\sum_{i=1}^n\frac{N_i}{N}\mathbf{E}(D_i)$

• $n$ 表示对特征 $A$，样本集合被划分为 $n$ 个不同的部分。（即 $A$ 中包含 $n$ 个不同的值）
• $N_i$ 表示第 $i$ 个部分的样本数量
• $\mathbf{E}(D_i)$ 表示特征 $A$ 下第 $i$ 个部分的分类集合的熵。

信息增益越大，分类后熵的值下降得越快，分类效果越好。

• 选择信息增益最大的特征属性进行分类。

C4.5

使用信息增益率进行衡量非纯度：

$\mathbf{GR}(D,A)=\frac{\mathbf{G}(D,A)}{\mathbf{SI}(D,A)}$

其中：

$\mathbf{SI}(D,A)=-\sum_{i=1}^n\frac{N_i}{N}\log_2\frac{N_i}{N}$

选择信息增益率最大的特征属性作为分类属性。

CART

分类树

针对特征属性 $A$，分类后的基尼指数为：

$\mathbf{Gini}_{sp}(D,A)=\sum_{i=1}^n\frac{N_i}{N}\mathbf{Gini}(D_i)$

选择分类基尼指数最小的特征属性作为分类属性。

当特征属性 $A$ 的取值大于2时（此处讨论二叉树），需要一个阈值 $\beta$，把 $D$ 分成 $D_1$ 和 $D_2$。设 $D_1$ 的样本数为 $L$，$D_2$ 的样本数为 $R$，
$L+R=N$。

$\mathbf{Gini}_{sp}(D,A^{(\beta)})=\frac{L}{N}\mathbf{Gini}(D_1)+\frac{R}{N}\mathbf{Gini}(D_2)$

$\mathbf{Gini}_{sp}(D,A^{(\beta)})=\frac{L}{N}\left(1-\frac{\sum_{j=1}^JL_j^2}{L^2}\right)+\frac{R}{N}\left(1-\frac{\sum_{j=1}^JR_j^2}{R^2}\right)\\ =\frac{1}{N}\left(L-\frac{\sum_{j=1}^JL_j^2}{L}+R-\frac{\sum_{j=1}^JR_j^2}{R}\right)\\ =1-\frac{1}{N}\left(\frac{\sum_{j=1}^JL_j^2}{L}+\frac{\sum_{j=1}^JR_j^2}{R}\right)$

• $\sum L_j=L$，$\sum R_j=R$

求 $\mathbf{Gini}_{sp}$ 最小值变成求下式的最大值：

$\mathbf{SG}(D,A^{(\beta)})\frac{\sum_{j=1}^JL_j^2}{L}+\frac{\sum_{j=1}^JR_j^2}{R}$

特征为类的分类树：

采集 20 个样本来构建是否踢球分类树，设出去踢球的响应值为 1，不踢球的响应值为 0，针对风力这个特征属性，响应值为 1 的样本有 14 个，无风有 6 个样本，小风有 5 个，中风 2 个，大风 1 个，则排序的结果为：大风<中风<小风<无风。然后依据这个顺序依次按照二叉树的分叉方式把样本分为左分支和右分支，并代入式求使该式为最大值的那个分叉方式，即先把是大风的样本放入左分支，其余的放入右分支，代入式，得到 A，再把大风和中风放入左分支，其余的放入右分支，代入式，得到 B，然后把大风、中风和小风放入左分支，无风的放入右分支，计算得到 C。比较 A、B、C，如果最大值为 C，则按照 C 的分叉方式划分左右分支，其中阈值 β 可以设为 3。

特征为数值的分类树：

如一共有 14 个样本，按照由小至大的顺序为abcdefghijklmn，第一次分叉为a|bcdefghijklmn，竖线“|”的左侧被划分到左分支，右侧被划分到右分支，代入式计算其值，然后第二次分叉为 ab|cdefghijklmn，同理代入式计算其值。依次类推，得到这 13 次分叉的最大值，该种分叉方式为最佳的分叉方式，其中阈值 β 为分叉的次数。

回归树

用均方误差代替熵计算：

$\mathbf{LS}(D)=\frac{1}{N}\sum_{i=1}^N(y_i-r_i)^2$

• $N$ 表示 $D$ 样本数量。
• $y_i$ 表示第 $i$ 个样本的输出值。
• $r_i$ 表示第 $i$ 个样本的预测值。

用样本输出值的平均值代替样本的预测值：

$\begin{aligned} \mathbf{LS} (D) &= \frac {1} {N} \sum_{i=1}^N \left( y_i - \frac {\sum_{i=1}^Ny_i} {N} \right) ^2 \\ &= \frac {1} {N} \sum_{i=1}^N \left[ y_i^2 - \frac {2y_i\sum_{i=1}^Ny_i} {N} + \frac {(\sum_{i=1}^Ny_i)^2} {N^2} \right] ^2 \\ &= \frac {1} {N} \left[ \sum_{i=1}^Ny_i^2 - \frac {2(\sum_{i=1}^Ny_i)^2} {N} + \frac {(\sum_{i=1}^Ny_i)^2} {N^2} \right] \\ &= \frac {1} {N} \left[ \sum_{i=1}^Ny_i^2 - \frac {(\sum_{i=1}^Ny_i)^2} {N} \right] \end{aligned}$

上式是集合 $D$ 的最小均方误差。如果针对某特征 $A$，则把集合 $D$ 划分为 $s$ 个部分，划分后的均方误差：

$\mathbf{LS}(D,A)=\sum_{i=1}^s\frac{N_i}{N}\mathbf{LS}(D_i)$

• $N_i$ 表示被划分的第 $i$ 个集合 $D_i$ 的样本数量。

集合 $D$ 的最小均方误差和划分后的均方误差的差值是划分为 $s$ 个部分后的误差减小量：

$\Delta\mathbf{LS}(D,A)=\mathbf{LS}(D)-\sum_{i=1}^s\frac{N_i}{N}\mathbf{LS}(D_i)$

此时需要寻求最大化的误差减小量，就得到最佳的 $s$ 个部分划分。

考虑二叉树，$s=2$。把 $D$ 分成 $D_1$ 和 $D_2$。设 $D_1$ 的样本数为 $L$，$D_2$ 的样本数为 $R$，$L+R=N$。

$\Delta\mathbf{LS}(D,A^{(\beta)})=\mathbf{LS}(D)-\frac{L}{N}\mathbf{LS}(D_1)-\frac{R}{N}\mathbf{LS}(D_2)$

$\begin{aligned} \Delta\mathbf{LS}(D,A^{(\beta)}) &=\frac{1}{N}\left[\sum_{i=1}^Ny_i^2-\frac{(\sum_{i=1}^Ny_i)^2}{N}\right]-\frac{L}{N}\left\{\frac{1}{L}\left[\sum_{i=1}^Ll_i^2-\frac{(\sum_{i=1}^Ll_i)^2}{L}\right]\right\}-\frac{R}{N}\left\{\frac{1}{R}\left[\sum_{i=1}^Rr_i^2-\frac{(\sum_{i=1}^Rr_i)^2}{R}\right]\right\}\\ &=\frac{1}{N}\left[\sum_{i=1}^Ny_i^2-\frac{(\sum_{i=1}^Ny_i)^2}{N}-\sum_{i=1}^Ll_i^2+\frac{(\sum_{i=1}^Ll_i)^2}{L}-\sum_{i=1}^Rr_i^2+\frac{(\sum_{i=1}^Rr_i)^2}{R}\right]\\ &=-\frac{(\sum_{i=1}^Ny_i)^2}{N^2}+\frac{1}{N}\left[\frac{(\sum_{i=1}^Ll_i)^2}{L}+\frac{(\sum_{i=1}^Rr_i)^2}{R}\right] \end{aligned}$

• $y_i$ 为集合 $D$ 的样本响应值。
• $l_i$ 为集合 $D_1$ 的样本响应值。
• $r_i$ 为集合 $D_2$ 的样本响应值。

上式除开定值，求上式最大值问题变成求下式最大值问题：

$\Delta\mathbf{LLS}(D,A^{(\beta)})=\frac{(\sum_{i=1}^Ll_i)^2}{L}+\frac{(\sum_{i=1}^Rr_i)^2}{R}$

特征为类的回归树：

• 计算每个特征属性各个种类的平均样本响应值，按大小进行排序，依次代入计算，得到最大值。

• 与特征为数值的分类树类似，按照数值大小顺序依次代入，得到最大值。

决策树缺失

分类树缺失响应值

如果想检测罕见的异常现象，而训练中包含的是大量正常现象，那么很可能分类结果就认为每种情况都是正常的。

可以通过设置先验概率，将异常情况的发生概率人为增加。

设 $Q_j$ 为设置的第 $j$ 个分类的先验概率，$N_j$ 为该分类的样本数，考虑样本率并进行归一化处理的先验概率 $q_j$ 为：

$q_j=\frac{Q_j/N_j}{\sum_{j=1}^J(Q_j/N_j)}$

代入分类树的式子，得到：

$\mathbf{SG}(D,A^{(\beta)},q)=\frac{\sum_{j=1}^J(q_jL_j)^2}{\sum_{j=1}^J(q_jL_j)}+\frac{\sum_{j=1}^J(q_jR_j)}{\sum_{j=1}^J(q_jR_j)}$

缺失特征属性

如果某些样本缺失了某个最佳分叉属性，如何解决：

1. 把该样本删除；
2. 使用各种算法估计缺失属性值；
3. 用另一个特征属性代替最佳分叉属性。

CART 采用的就是计算替代分叉属性，防止最佳分叉属性缺失。

决策树剪枝

剪枝：去掉一些结点，包括叶结点和中间结点，简化树。

• 预剪枝：构建树过程中，提前终止决策树的生长；
• 后剪枝：构建树后去掉一些结点。
  • 悲观错误剪枝（PEP）
  • 最小错误剪枝（MEP）
  • 代价复杂度剪枝（CCP）
  • 基于错误剪枝（EBP）

CCP 算法会产生一系列树的序列 $\{T_0,T_1,\cdots,T_m\}$，$T_0$ 是由训练得到的最初的完整决策树，$T_m$ 只含有一个根节点，序列中的树是嵌套的，即 $T_{i+1}$ 由 $T_i$ 剪枝得到的。

• 用 $T_{i+1}$ 中的一个叶结点替代 $T_i$ 中以该节点为根的子树。

替代的原则就是使误差的增加率 $\alpha$ 最小：

$\alpha=\frac{\mathbf{R}(n)-\mathbf{R}(n_t)}{\vert n_t\vert-1}$

• $\mathbf{R}(n)$ 表示 $T_i$ 中结点 $n$ 的预测误差；
• $\mathbf{R}(n_t)$ 表示 $T_i$ 中以结点 $n$ 为根结点的子树的所有叶结点的预测误差之和；
• $\vert n_t\vert$ 表示该子树叶结点的数量，$n_t$ 也被称为复杂度。
• $\alpha$ 的含义是用一个结点 $n$ 来替代以 $n$ 为根节点的所有 $\vert n_t\vert$ 个结点的误差增加的规范化程度。

在 $T_i$ 中，选择最小的 $\alpha$ 值的结点进行替代，得到 $T_{i+1}$。每需要得到一棵决策树，都需要计算其前一棵决策树的 $\alpha$ 值，根据 $\alpha$ 值进行剪枝，最终直至 $T_m$。

分类树的情况，如果使用分类误差来表示结点 $n$ 的预测误差，则：

$\mathbf{R}(n)=\frac{\sum_{j=1}^mN_j-\max{\{N_j\}}}{\sum_{j=1}^mN_j}=\frac{N-\max{\{N_j\}}}{N}$

• $N_j$ 表示结点 $n$ 下第 $j$ 个分类的样本数；
• $N$ 表示该结点的所有样本数；
• $\max{\{N_j\}}$ 表示在 $m$ 个分类中，拥有样本数最多的那个分类的样本数量。

回归树的情况，可以使用集合 $D$ 的最小均方误差表示结点 $n$ 的预测误差：

$\mathbf{R}(n)=\frac{\sum_{i=1}^N(y_i^2)-\frac{(\sum_{i=1}^Ny_i)^2}{N}}{N}$

• $y_i$ 表示第 $i$ 个样本的响应值；
• $N$ 为该结点的样本数量。

用全部样本得到的决策树序列为 $\{T_0,T_1,\cdots,T_m\}$，其对应值 $\alpha_0<\alpha_1<\cdots<\alpha_m$。下一步是从这个序列最优选择一颗决策树 $T_i$，常用交叉验证法。

OpenCV提供的DTree

DTrees 类表示一个决策树或一组决策树。类的当前公共接口允许用户只训练单个决策树，但是类能够存储多个决策树并使用它们进行预测(通过求和响应或使用投票方案)，以及从DTree类派生的类（如RTree和Boost）使用此功能来实现决策树集成。

该类中有部分参数解释：

• MaxCategories：表示特征属性为类的形式的最大类数量。如果训练过程中，类的数量大于该值，采用聚类方法更高效。该参数只应用于非两类的分类树问题。通过以下函数访问：

1
2

int getMaxCategories();
void setMaxCategories(int val);

• MaxDepth：决策树的最大可能深度。通过以下函数访问：

1
2

int getMaxDepth();
void setMaxDepth(int val);

• MinSampleCount：如果某个结点的样本数小于该值，则该结点不再被分叉。通过以下函数访问：

1
2

int getMinSampleCount();
void setMinSampleCount(int val);

• CVFolds：表示交叉验证的子集数量。如果值大于1，则应该交叉验证进行剪枝。通过以下函数访问：

1
2

int getCVFolds();
void setCVFolds(int val);

• UseSurrogates：如果设为真，则需要产生代替分叉节点。默认为假。通过以下函数访问：

1
2

bool getUseSurrogates();
void setUseSurrogates(bool val);

• Use1SERule：如果设为真，表示剪枝过程使用 1SE 规则，使决策树更加的，且对训练集的噪声更有抵抗力，但精度会下降。默认为真。通过以下函数访问：

1
2

bool getUse1SERule();
void setUse1SERule(bool val);

• TruncatePrunedTree：如果设为真，则要被剪掉的结点将从树上移除，否则仍保留。默认为真。通过以下函数访问：

1
2

bool getTruncatePrunedTree();
void setTruncatePrunedTree(bool val);

• RegressionAccuracy：构建回归树的条件，表示回归树的响应值的精度如果达到该值则无需再分叉。通过以下函数访问：

1
2

float getRegressionAccuracy();
void setRegressionAccuracy(float val);

• Priors：表示分类树的类别标签先验概率，按类别标签值排序。通过以下函数访问：

1

cv::Mat getPriors()void setPriors(const cv::Mat &val);

例子-单词难度预测

数据集地址：https://aistudio.baidu.com/datasetdetail/107161

数据集属性有：

• Word：单词
• Length：长度
• Freq_HAL：频率_HAL
• Log_Freq_HAL：对数频率HAL
• I_Mean_RT
• I_Zscore：确定单词的难度。对于一个单词，此值在0和1之间波动，其中0为简单，1为困难
• I_SD
• Obs
• I_Mean_Accuracy：准确性，为响应值

部分数据如下：

效果如下：

1
2
3
4
5

Train Data imported: 30457
Test Data imported: 9992
决策树算法(基于OpenCV实现)：
计算花费时长：159ms
平均误差：0.0239817

代码地址：Gitee - Decision Tree