讨论使用空间滤波器进行图像处理。

线性空间滤波

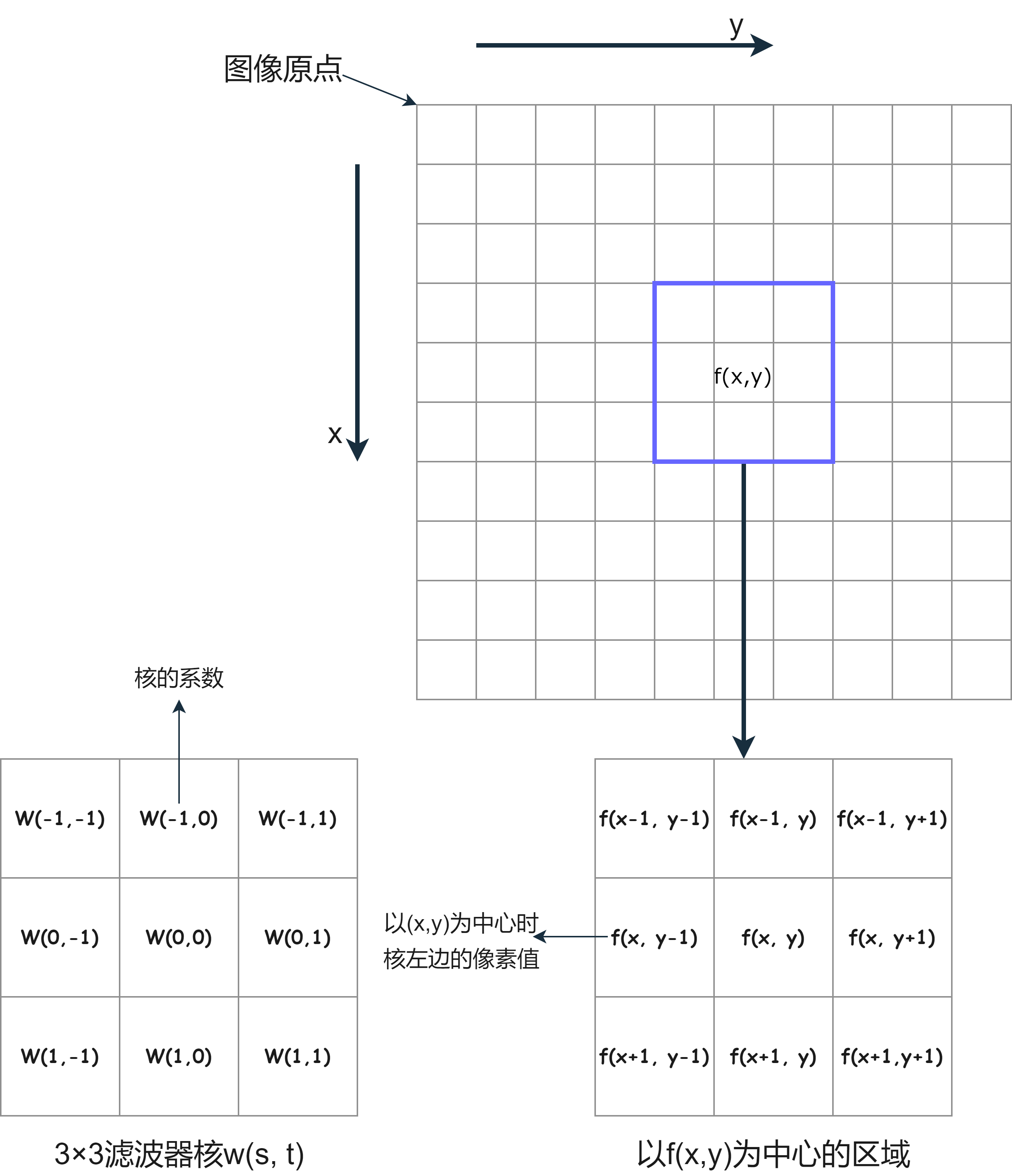
线性空间滤波器在图像f和滤波器核w之间执行乘积之和运算。

滤波器核（或称核）是一个阵列，其大小定义了运算的邻域，其系数决定了该滤波器的性质。

使用3×3核进行线性空间滤波原理

在上图的任何一点(x, y)处，滤波器的响应g(x, y)是核系数与核所覆盖图像像素的乘积之和：

g(x,y)=w(−1,−1)f(x−1,y−1)+w(−1,0)f(x−1,y)+…+w(1,1)f(x+1,y+1)g(x,y) = w(-1,-1)f(x-1,y-1)+w(-1,0)f(x-1,y)+…+w(1,1)f(x+1, y+1)

坐标x和y变化时，核的中心逐个像素移动，并在移动过程中生成了滤波后的图像g。

核中心系数w(0,0)对其于(x,y)处的像素，当大小为m×n的核，假设m=2a+1，n=2b+1，a和b非负。这意味着这是两个坐标方向上奇数大小的核。

一般而言，大小为m×n的核对大小为M×N的图像的线性空间滤波可以表示为：

g(x,y)=∑s=−aa∑t=−bbw(s,t)f(x+s,y+t)g(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)

在上式中，x和y发生变化时，核的原点可以访问图像的每个像素。当x和y不变时，上式即乘积之和，只适合任意奇数大小的核。

空间相关与卷积

对于式子：

g(x,y)=∑s=−aa∑t=−bbw(s,t)f(x+s,y+t)g(x,y) = \sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)

化简为一维讨论：

g(x)=∑s=−aaw(s)f(x+s)g(x) = \sum_{s=-a}^aw(s)f(x+s)

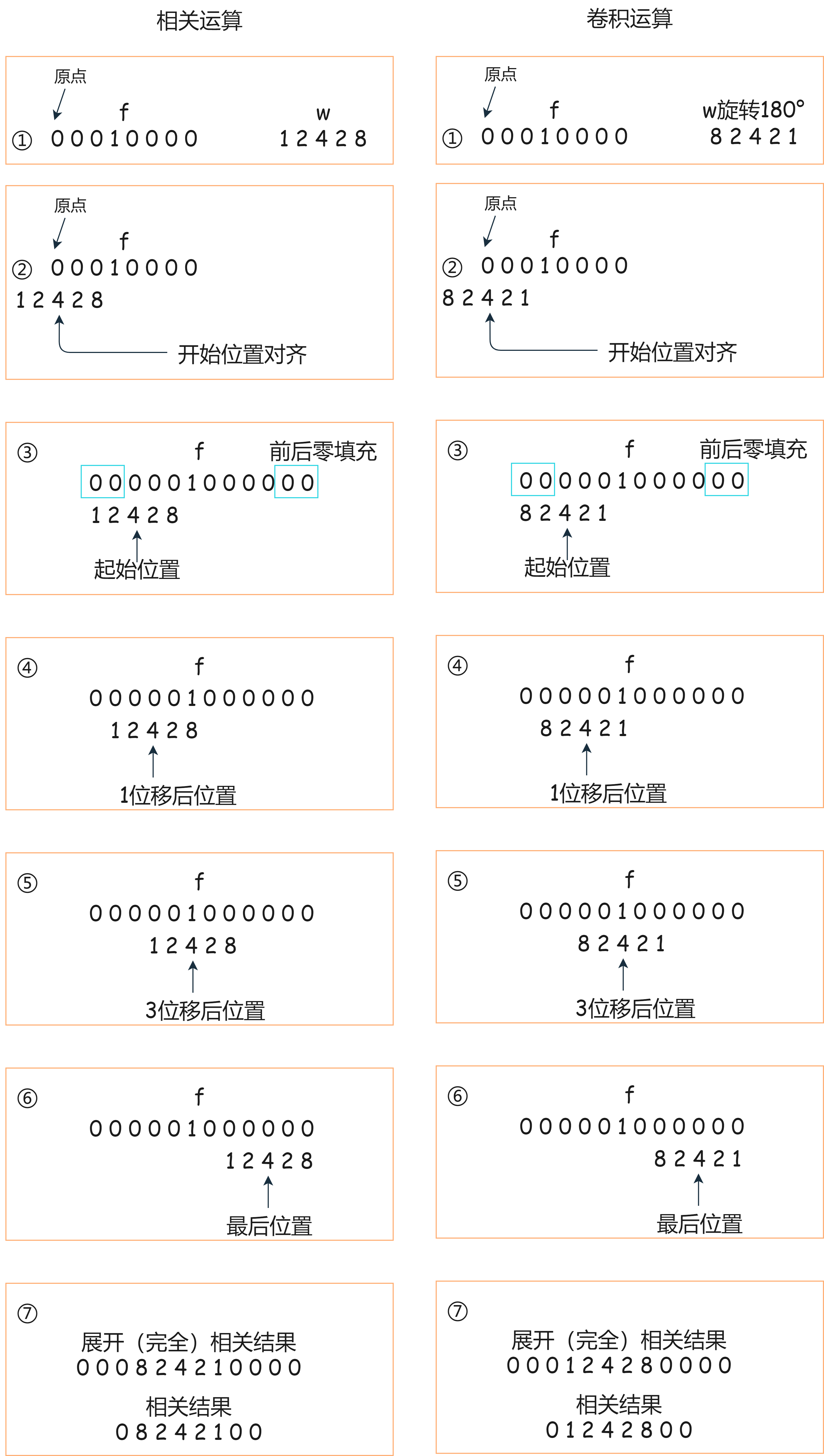
举一个一维例子：核w为 1 2 4 2 8

相关 是滤波器核相对于图像的位移的函数，即相关的第一个值对应于核的零位移，第二个值对应于核的1单位位移。

卷积 是滤波器核先进行预旋转，再进行相对于图像位移的函数。

①该核大小为 1×51\times 5，那么有a=2，b=0。

②w中心系数要与f的原点重合。

③w的一部分在f之外，求和不能运算，所以进行零补充（零补充不是唯一选择）。如果核大小为1×m，那么在两侧都需要补 (m−1)/2(m-1)/2 个0。

接下来根据移动和式计算：

g(x)=∑s=−aaw(s)f(x+s)g(0)=∑s=−22w(s)f(s+0)=0g(1)=∑s=−22w(s)f(s+1)=8g(2)=∑s=−22w(s)f(s+2)=2g(3)=∑s=−22w(s)f(s+3)=4g(4)=∑s=−22w(s)f(s+4)=2g(5)=∑s=−22w(s)f(s+5)=1g(6)=∑s=−22w(s)f(s+6)=0g(7)=∑s=−22w(s)f(s+7)=0g(x) = \sum_{s=-a}^aw(s)f(x+s)\\ g(0) = \sum_{s=-2}^2w(s)f(s+0) = 0\\ g(1) = \sum_{s=-2}^2w(s)f(s+1) = 8\\ g(2) = \sum_{s=-2}^2w(s)f(s+2) = 2\\ g(3) = \sum_{s=-2}^2w(s)f(s+3) = 4\\ g(4) = \sum_{s=-2}^2w(s)f(s+4) = 2\\ g(5) = \sum_{s=-2}^2w(s)f(s+5) = 1\\ g(6) = \sum_{s=-2}^2w(s)f(s+6) = 0\\ g(7) = \sum_{s=-2}^2w(s)f(s+7) = 0\\

另外，把一个元素是1，其余元素是0的函数称为 离散单位冲激函数。而核与离散单位冲激函数进行 相关 时，会在这个冲激的位置产生核的旋转版本。

广泛地说，一个函数与一个冲激进行卷积时，在冲激所在的位置产生这个函数的副本。

将一维推广到二维图像，对于大小为m×n的核，需要在图像的顶部核底部至少补 (m−1)/2(m-1)/2 行0，在左侧和右侧至少补 (n−1)/2(n-1)/2 列0。

假设m和n都为3：

二维下的旋转180°等效于核关于其一个轴旋转，再关于另一个轴旋转。

回头再看冲激函数，其坐标 (x0,y0)(x_0,y_0) 处的离散冲激强度（振幅）A定义为：

δ(x−x0,y−y0)={A,x0=x和y0=y0,othersδ(x-x_0,y-y_0)=\left\{ \begin{matrix} A,&x_0=x和y_0=y\\ 0,&others \end{matrix} \right.

小结

大小为m×n的核w与图像f(x,y)的相关：

w☆f(x,y)=(w☆f)(x,y)=∑s=−aa∑t=−bbw(s,t)f(x+s,y+t)w☆f(x,y)=(w☆f)(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x+s,y+t)

大小为m×n的核w与图像f(x,y)的卷积：

w★f(x,y)=(w★f)(x,y)=∑s=−aa∑t=−bbw(s,t)f(x−s,y−t)w★f(x,y)=(w★f)(x,y)=\sum_{s=-a}^a\sum_{t=-b}^bw(s,t)f(x-s,y-t)

当卷积其中的一个函数旋转180°后，减号对应其f和w的坐标，也可以完成乘积之和处理即线性空间滤波。

相关和卷积运算满足的性质：

性质 卷积 相关
交换律 f★g = g★f 不成立
结合律 f★(g★h) = (f★g)★h 不成立
分配律 f★(g+h)=(f★g)+(f★h) f☆(g+h)=(f☆g)+(f☆h)

低通空间滤波器

盒式滤波器、均值滤波器

均值滤波就是将区域内的像素灰度值的平均值作为中心像素的灰度值。

一个3×3的均值滤波器核如：

11119×111111\qquad 1\qquad1\qquad1\\ \frac 19\times 1\qquad 1\qquad1\\ \qquad 1\qquad1\qquad1

OpenCV提供了一个均值滤波（盒式滤波器）函数；

1
2
3
4
5
void blur(InputArray src,
		  OutputArray dst,
		  Size ksize,
		  Point anchor = Point(-1,-1),
		  int borderType = BORDER_DEFAULT)

参数如下：

  • src：输入图像; 它可以有任意数量的通道，这些通道是独立处理的，但深度应该是CV_8U, CV_16U, CV_16S, CV_32F或CV_64F。

  • dst：输出与src相同大小和类型的图像。

  • ksize：核大小，cv::Size类型。

  • anchor：锚点，默认值Point(-1，-1)表示锚点位于内核中心。

  • borderType：int类型，用于推断图像外部像素的某种边界模式，一般不管。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <opencv2/opencv.hpp>
#include <iostream>

// 手动实现盒式均值滤波器
void filter(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;  // 实现对齐核中心元素
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            int sum = 0;    // 计算相关
            for (int m = -k; m < k + 1; m ++)
                for (int n = -k; n < k + 1; n ++)
                    sum += image_input.at<uchar>(i + m, j + n);

            image_output.at<uchar>(i, j) = round(sum / (filter_size * filter_size));
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg", 0);
    cv::Mat image_output, image_output2;

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    // CV自带的均值滤波器，核大小为7
    cv::blur(image, image_output, cv::Size(7, 7));
    // 自己实现的均值滤波器，核大小为7
    filter(7, image, image_output2);

    // 对比CV自带的均值滤波器与自己实现的均值滤波器性能表现
    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

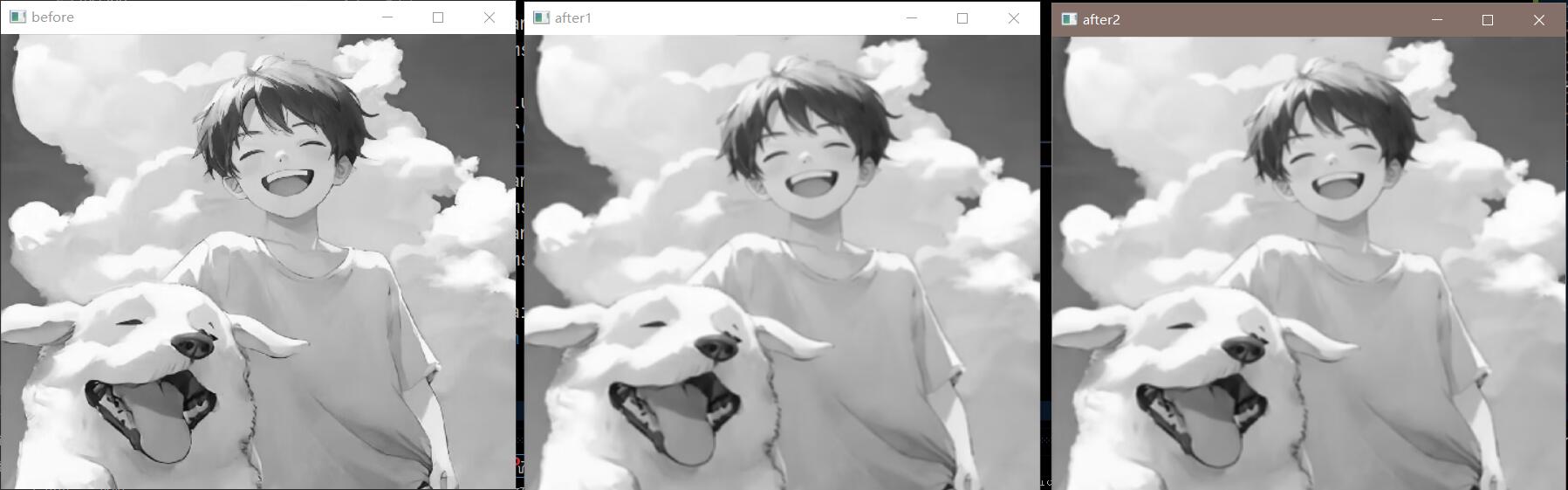
效果展示

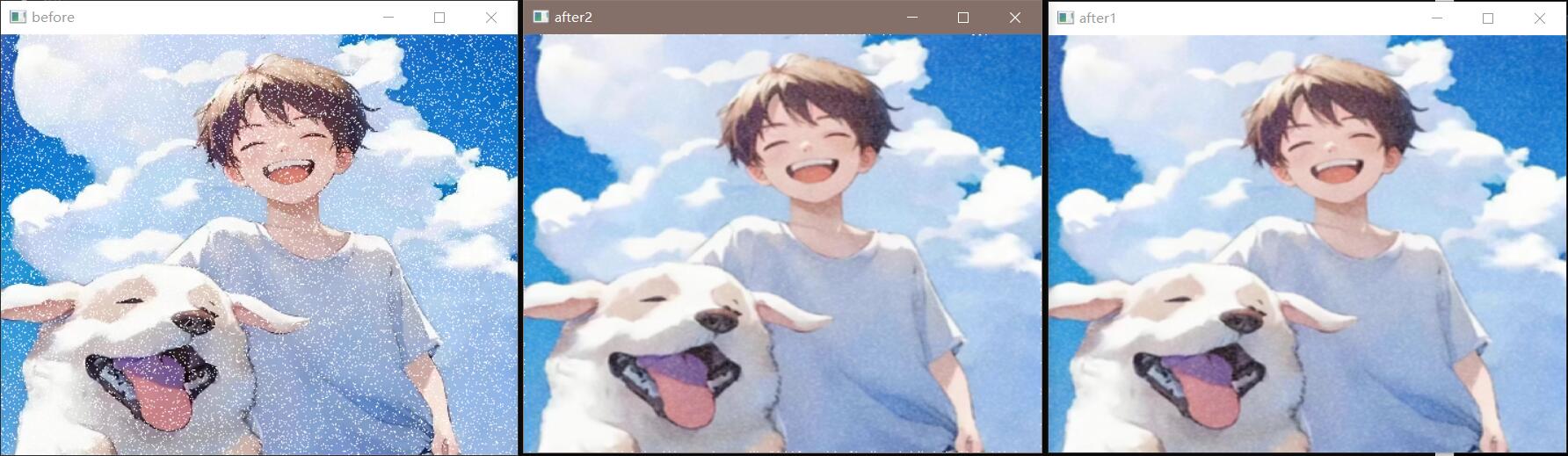
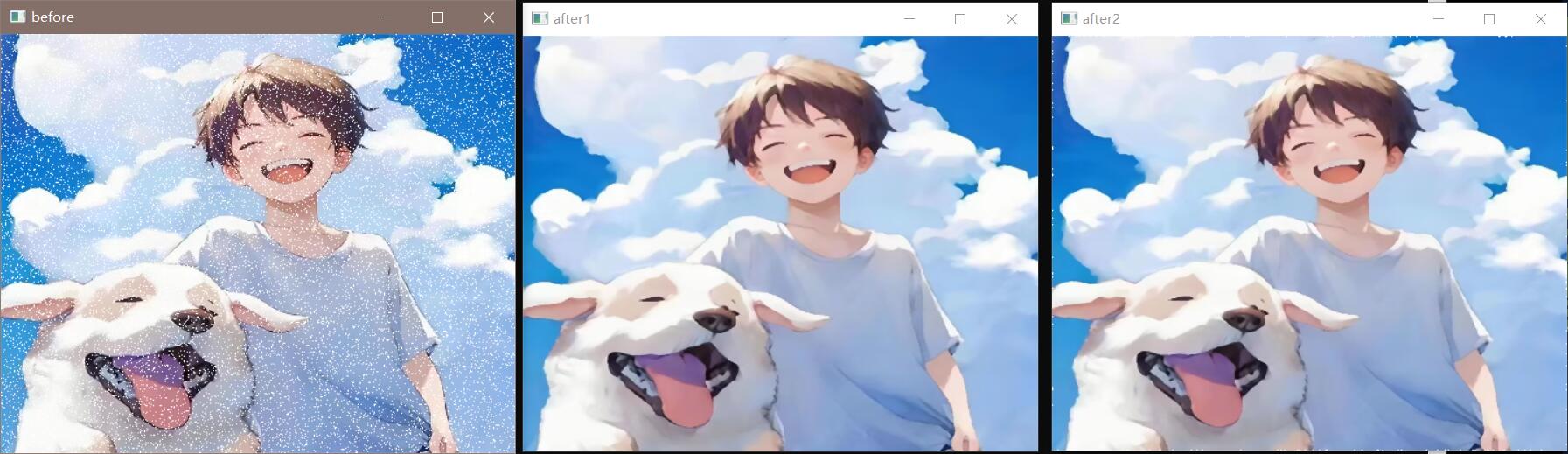
也许上述效果不明显，可以进行彩色图像，增加杂波，再进行均值滤波器处理。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include <opencv2/opencv.hpp>
#include <iostream>
#include <random>

// 随机将n个像素值变成白点，构成噪声
void Salt(cv::Mat image, int n)
{
    // 生成随机数
    std::default_random_engine generater;
    std::uniform_int_distribution<int>randomRow(0, image.rows - 1);
    std::uniform_int_distribution<int>randomCol(0, image.cols - 1);

    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = randomRow(generater);
        j = randomCol(generater);
        if (image.channels() == 1)
            image.at<uchar>(i, j) = 255;
        if (image.channels() == 3)
        {
            image.at<cv::Vec3b>(i, j)[0] = 255;
            image.at<cv::Vec3b>(i, j)[1] = 255;
            image.at<cv::Vec3b>(i, j)[2] = 255;
        }
    }
}

// 手动实现均值滤波器，BGR三通道都进行均值滤波
void filter(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            int sum1 = 0, sum2 = 0, sum3 = 0;
            for (int m = -k; m < k + 1; m ++)
            {
                for (int n = -k; n < k + 1; n ++)
                {
                    sum1 += image_input.at<cv::Vec3b>(i + m, j + n)[0];
                    sum2 += image_input.at<cv::Vec3b>(i + m, j + n)[1];
                    sum3 += image_input.at<cv::Vec3b>(i + m, j + n)[2];
                }

            }
            image_output.at<cv::Vec3b>(i, j)[0] = round(sum1 / (filter_size * filter_size));
            image_output.at<cv::Vec3b>(i, j)[1] = round(sum2 / (filter_size * filter_size));
            image_output.at<cv::Vec3b>(i, j)[2] = round(sum3 / (filter_size * filter_size));
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat image_output, image_output2;
    Salt(image, 100000);    // 随机生成10w个白点构成噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    cv::blur(image, image_output, cv::Size(7, 7));
    filter(7, image, image_output2);

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示

高斯滤波器

在统计学与概率论中，高斯函数是正态分布（高斯分布）的密度函数。一维的高斯表达式如下：

f(x)=ae−(x−μ)22σ2f(x)=ae^{-\frac{(x-μ)^2} {2σ^2} }\\

其中a、μ、σ为实数常数，a>0；a表示曲线的高度，μ表示曲线在x轴的中心，σ与半峰全宽有关。

而二维高斯表达式如下：

G(x,y)=12πσ2e−−(x2+y2)2σ2G(x,y)=\frac{1} {2\piσ^2}e^{-\frac{-(x^2+y^2)} {2σ^2} }

故高斯核为：

w(s,t)=G(s,t)=Ke−s2+t22σ2G(r)=Ke−r22σ2，当r=(s2+t2)12w(s,t)=G(s,t)=Ke^{-\frac{s^2+t^2} {2σ^2} }\\ G(r)=Ke^{-\frac{r^2} {2σ^2} }，当r=(s^2+t^2)^{\frac 12}

OpenCV提供了一个高斯滤波器函数；

1
2
3
4
5
6
void GaussianBlur( InputArray src,
				   OutputArray dst,
				   Size ksize,
				   double sigmaX,
				   double sigmaY = 0,
				   int borderType = BORDER_DEFAULT )

参数如下：

  • src：输入图像; 它可以有任意数量的通道，这些通道是独立处理的，但深度应该是CV_8U, CV_16U, CV_16S, CV_32F或CV_64F。

  • dst：输出与src相同大小和类型的图像。

  • ksize：核大小，cv::Size类型。

  • sigmaX：高斯核函数在X方向上的标准偏差。

  • sigmaY：高斯核函数在Y方向上的标准偏差。如果sigmaY为0，则将其设为sigmaX；如果sigmaX核sigmaY都为0，则有ksize.width核ksize.height计算。

  • borderType：int类型，用于推断图像外部像素的某种边界模式，一般不管。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <opencv2/opencv.hpp>
#include <iostream>
#include <random>
#include <cmath>

// 随机将n个像素值变成白点，构成噪声
void Salt(cv::Mat image, int n)
{
    // 生成随机数
    std::default_random_engine generater;
    std::uniform_int_distribution<int>randomRow(0, image.rows - 1);
    std::uniform_int_distribution<int>randomCol(0, image.cols - 1);

    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = randomRow(generater);
        j = randomCol(generater);
        if (image.channels() == 1)
            image.at<uchar>(i, j) = 255;
        if (image.channels() == 3)
        {
            image.at<cv::Vec3b>(i, j)[0] = 255;
            image.at<cv::Vec3b>(i, j)[1] = 255;
            image.at<cv::Vec3b>(i, j)[2] = 255;
        }
    }
}

// 手动实现高斯滤波器，BGR三通道都进行高斯滤波
void filter1(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            double sum1 = 0.0, sum2 = 0.0, sum3 = 0.0;
            double sum1_ = 0.0, sum2_ = 0.0, sum3_ = 0.0;
            double sigma = 7, g;   // sigma可修改
            for (int m = -k; m < k + 1; m ++)
            {
                for (int n = -k; n < k + 1; n ++)
                {
                    g = exp(-(m * m + n * n) / (2 * sigma * sigma));
                    sum1 += g * image_input.at<cv::Vec3b>(i + m, j + n)[0];
                    sum1_ += g;
                    sum2 += g * image_input.at<cv::Vec3b>(i + m, j + n)[1];
                    sum2_ += g;
                    sum3 += g * image_input.at<cv::Vec3b>(i + m, j + n)[2];
                    sum3_ += g;
                }

            }
            image_output.at<cv::Vec3b>(i, j)[0] = (int) round(sum1 / sum1_);
            image_output.at<cv::Vec3b>(i, j)[1] = (int) round(sum2 / sum2_);
            image_output.at<cv::Vec3b>(i, j)[2] = (int) round(sum3 / sum3_);
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat image_output, image_output2;
    Salt(image, 100000);    // 随机生成10w个白点构成噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    cv::GaussianBlur(image, image_output, cv::Size(7, 7), 2, 2);
    filter1(7, image, image_output2);

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

效果展示

中值滤波

中值滤波就是取周围邻域像素灰度值（或GRB值）的中值作为中心像素灰度值结果。

OpenCV提供了一个中值滤波器函数；

1
void medianBlur(InputArray src, OutputArray dst, int ksize)

参数如下：

  • src：输入图像; 输入1、3或4通道图像，当ksize为3或5时，图像深度应该是CV_8U、CV_16U或CV_32F，对于更大的孔径尺寸，只能是CV_8U。

  • dst：输出与src相同大小和类型的图像。

  • ksize：核大小。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <opencv2/opencv.hpp>
#include <iostream>
#include <random>
#include <cmath>

// 随机将n个像素值变成白点，构成噪声
void Salt(cv::Mat image, int n)
{
    // 生成随机数
    std::default_random_engine generater;
    std::uniform_int_distribution<int>randomRow(0, image.rows - 1);
    std::uniform_int_distribution<int>randomCol(0, image.cols - 1);

    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = randomRow(generater);
        j = randomCol(generater);
        if (image.channels() == 1)
            image.at<uchar>(i, j) = 255;
        if (image.channels() == 3)
        {
            image.at<cv::Vec3b>(i, j)[0] = 255;
            image.at<cv::Vec3b>(i, j)[1] = 255;
            image.at<cv::Vec3b>(i, j)[2] = 255;
        }
    }
}

// 找中值
cv::Vec3b MedianFinding(cv::Mat &mat, int filter_size)
{
    cv::Vec3b tmp;
    cv::Vec3b m;
    for (int i = 1; i <= filter_size - 1; i++)
    {
        for (int j = 1; j <= filter_size - i; j++)
        {
            if (mat.at<cv::Vec3b>(j - 1)[0] > mat.at<cv::Vec3b>(j)[0])
            {
                tmp = mat.at<cv::Vec3b>(j - 1);
                mat.at<cv::Vec3b>(j - 1) = mat.at<cv::Vec3b>(j);
                mat.at<cv::Vec3b>(j) = tmp;
            }
        }
    }
    return m = mat.at<cv::Vec3b>((filter_size + 1) / 2);
}

// 手动实现中值滤波器，BGR三通道都进行中值滤波
void filter2(int filter_size, cv::Mat &image_input, cv::Mat &image_output)
{
    image_output = image_input.clone();
    int k = (filter_size - 1) / 2;
    cv::Mat arry(1, filter_size * filter_size, CV_8UC3);
    for (int i = k; i < image_input.rows - k; i ++)
    {
        for (int j = k; j < image_input.cols - k; j ++)
        {
            int mid = 0;
            for (int m = -k; m < k + 1; m ++)
            {
                for (int n = -k; n < k + 1; n ++)
                {
                    arry.at<cv::Vec3b>(mid) = image_input.at<cv::Vec3b>(i + m, j + n);
                    mid ++;
                }
            }
            image_output.at<cv::Vec3b>(i, j) = MedianFinding(arry, filter_size * filter_size);
        }
    }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg");
    cv::Mat image_output, image_output2;
    Salt(image, 100000);    // 随机生成10w个白点构成噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    cv::medianBlur(image, image_output, 7);
    filter2(7, image, image_output2);   // 个人体验速度较慢

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

效果展示

高通空间滤波器

高通基础

锐化的作用时突出灰度中的过渡。

平滑可以类似为积分运算，那么锐化则可以类似为微分运算。图像模糊在空间域中可以通过平均（平滑）一个邻域中的像素实现。而图像微分将会增强边缘和其他不连续（如噪声）。

数字函数的导数是用差分定义，一阶导数的任何定义都要满足：

  1. 恒定灰度区域的一阶导数必须为零。

  2. 灰度台阶或斜坡开始处的一阶导数必须非零。

  3. 灰度斜坡上的一阶导数必须非零。

类似有二阶导数的任何定义都要满足：

  1. 恒定灰度区域的二阶导数必须为零。

  2. 灰度台阶或斜坡的开始处和结束处的二阶导数必须非零。

  3. 灰度斜坡上的二阶导数必须为零。

而处理图像时，变化发生的最短距离也就是像素间的距离。

一维函数 f(x)f(x) 的一阶导数的一个基本定义是差分：

dfdx=f(x+1)−f(x)\frac {\mathrm{d}f} {\mathrm{d}x}=f(x+1)-f(x)

二维函数 f(x,y)f(x,y) 的二阶导数定义为差分：

∂2f∂x2=f(x+1)+f(x−1)−2f(x)\frac {\partial^2 f} {\partial x^2}=f(x+1)+f(x-1)-2f(x)

先用一维函数举例：

一维函数导数满足上述性质，类比一维函数可知二维函数。数字图像的边缘在灰度上通常类似于斜坡过渡，图像的一阶导数会产生较宽的边缘；另外，二阶导数会产生宽度为1像素并由零分隔的双边缘。所以， 与一阶导数相比，二阶导数可增强更精细的细节，而实现二阶导数所需的运算量也更少。

拉普拉斯锐化滤波

最简单的各向同性导数算子（核）是拉普拉斯。 对于两个变量的函数 f(x,y)f(x,y) ，定义为：

∇2f=∂2f∂x2+∂2f∂y2\nabla^2f=\frac {\partial^2f} {\partial x^2} + \frac {\partial^2f} {\partial y^2}

拉普拉斯是线性算子。在x方向有：

∂2f∂x2=f(x+1,y)+f(x−1,y)−2f(x,y)\frac{\partial^2f} {\partial x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)

在y方向有：

∂2f∂x2=f(x,y+1)+f(x,y−1)−2f(x,y)\frac{\partial^2f} {\partial x^2}=f(x,y+1)+f(x,y-1)-2f(x,y)

由上面三个式子可得两个变量的拉普拉斯是：

∇2f(x,y)=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x,y)\nabla^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)

该公式可以使用卷积运算，上式的拉普拉斯核为：

0101−41010(a)\begin{matrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{matrix}\tag{a}

这个也叫四邻域核，还有八邻域核：

1111−81111(b)\begin{matrix} 1 & 1 & 1 \\ 1 & -8 & 1 \\ 1 & 1 & 1 \end{matrix}\tag{b}

两个其他的核（系数反转）：

0−10−14−10−10(c)\begin{matrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{matrix}\tag{c}

−1−1−1−18−1−1−1−1(d)\begin{matrix} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \end{matrix}\tag{d}

但是不能直接使用拉普拉斯，它会突出图像中急剧灰度过渡，不强调缓慢变化的灰度区域，往往会产生具有灰色边缘线核其他不连续的图像。所以需要 将拉普拉斯图像和原图像相加恢复背景特征。

使用拉普拉斯锐化图像：

g(x,y)=f(x,y)+c[∇2f(x,y)]g(x,y)=f(x,y)+c[\nabla^2f(x,y)]

f(x,y)为输入图像，g(x,y)为锐化后图像。若使用核 a 或核 b，取c=-1；若使用核 c 或核 d，取c=1。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <opencv2/opencv.hpp>
#include <iostream>

// 四邻域拉普拉斯核
void filter_4(cv::Mat &input, cv::Mat &output)
{
    output = input.clone();
    int la;
    for (int i = 1; i < input.rows - 1; i ++)
        for (int j = 1; j < input.cols - 1; j ++)
        {
            la = input.at<uchar>(i + 1, j) + input.at<uchar>(i - 1, j)
                + input.at<uchar>(i, j + 1) + input.at<uchar>(i, j - 1)
                - 4 * input.at<uchar>(i, j);
            output.at<uchar>(i, j) = cv::saturate_cast<uchar>(output.at<uchar>(i, j) - la);
        }
}

// 八邻域拉普拉斯核
void filter_8(cv::Mat &input, cv::Mat &output)
{
    output = input.clone();
    int la;
    for (int i = 1; i < input.rows - 1; i ++)
        for (int j = 1; j < input.cols - 1; j ++)
        {
            la = input.at<uchar>(i - 1, j - 1) + input.at<uchar>(i - 1, j) +
                input.at<uchar>(i - 1, j + 1) + input.at<uchar>(i, j - 1) +
                input.at<uchar>(i, j + 1) + input.at<uchar>(i + 1, j - 1) +
                input.at<uchar>(i + 1, j) + input.at<uchar>(i + 1, j + 1) -
                8 * input.at<uchar>(i, j);
            output.at<uchar>(i, j) = cv::saturate_cast<uchar>(output.at<uchar>(i, j) - la);
        }
}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg", 0);
    cv::Mat image_output, image_output2;

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);

    filter_4(image, image_output);
    filter_8(image, image_output2);

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", image_output);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", image_output2);

    cv::waitKey(0);
    return 0;
}

拉普拉斯锐化滤波对于灰度图像的影响十分明显，但是对于彩色图像影响一般。如果想改为适用于彩色图像，只需将数据类型从 uchar 改为 cv::Vec2b。

效果展示：

效果展示

一阶导数锐化——梯度

一阶导数是用梯度幅度实现。图像f在坐标(x,y)处的梯度定义为二维列向量：

∇f≡grad(f)=[gxgy]=[∂f/∂x∂f/∂y]\nabla f\equiv grad(f)=\left[\begin{matrix}g_x \\ g_y\end{matrix}\right]=\left[\begin{matrix}\partial f/\partial x \\ \partial f/\partial y\end{matrix}\right]

这个向量指向f的最大变化率方向。

向量 ∇f\nabla f 的幅度（长度）表示为M(x,y)（有时候用 ∣∣∇f∣∣\vert\vert\nabla f\vert\vert ），其中

M(x,y)=∣∣∇f∣∣=mag(∇f)=gx2+gy2M(x,y)=\vert\vert\nabla f\vert\vert=mag(\nabla f)=\sqrt{g_x^2+g_y^2}

是梯度向量方向的变化率在(x,y)处的值，方向为：

α(x,y)=tan⁡−1[gy(x,y)gx(x,y)]\alpha(x,y)=\tan^{-1}\left[\begin{matrix}\frac{g_y(x,y)} {g_x(x,y)}\end{matrix}\right]

而M(x,y)是与原图像大小相同的图像，也称为梯度图像。

梯度常用于检测边缘，在边缘检测会详细介绍。

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。