图像边缘检测

边缘检测的步骤

  1. 为了降低噪声，对图像进行平滑处理。

  2. 检测边缘点。

  3. 边缘定位。

图像梯度

计算图像f在任意位置(x, y)处的边缘强度和方向的工具是梯度。

定义梯度为向量：

∇f(x,y)≡grad[f(x,y)]≡[gx(x,y)gy(x,y)]=[∂f(x,y)∂x∂f(x,y)∂y]\nabla f(x,y)\equiv grad[f(x,y)]\equiv \left[ \begin{matrix} g_x(x,y)\\ g_y(x,y)\\ \end{matrix} \right]= \left[ \begin{matrix} \frac{\partial f(x,y)} {\partial x}\\ \frac{\partial f(x,y)} {\partial y}\\ \end{matrix} \right]

根据梯度向量求点(x,y)处方向变化率的值：

M(x,y)=∣∣∇f(x,y)∣∣=gx2(x,y)+gy2(x,y)M(x,y) = \vert\vert\nabla f(x,y)\vert\vert=\sqrt{g_x^2(x,y)+g_y^2(x,y)}

其中M(x,y)称为图像f的梯度图像。

上式变化率方向为：

α(x,y)=tan⁡−1[gy(x,y)gx(x,y)]\alpha(x,y)=\tan^{-1}\Big[\frac{g_y(x,y)} {g_x(x,y)}\Big]

常见梯度算子有：

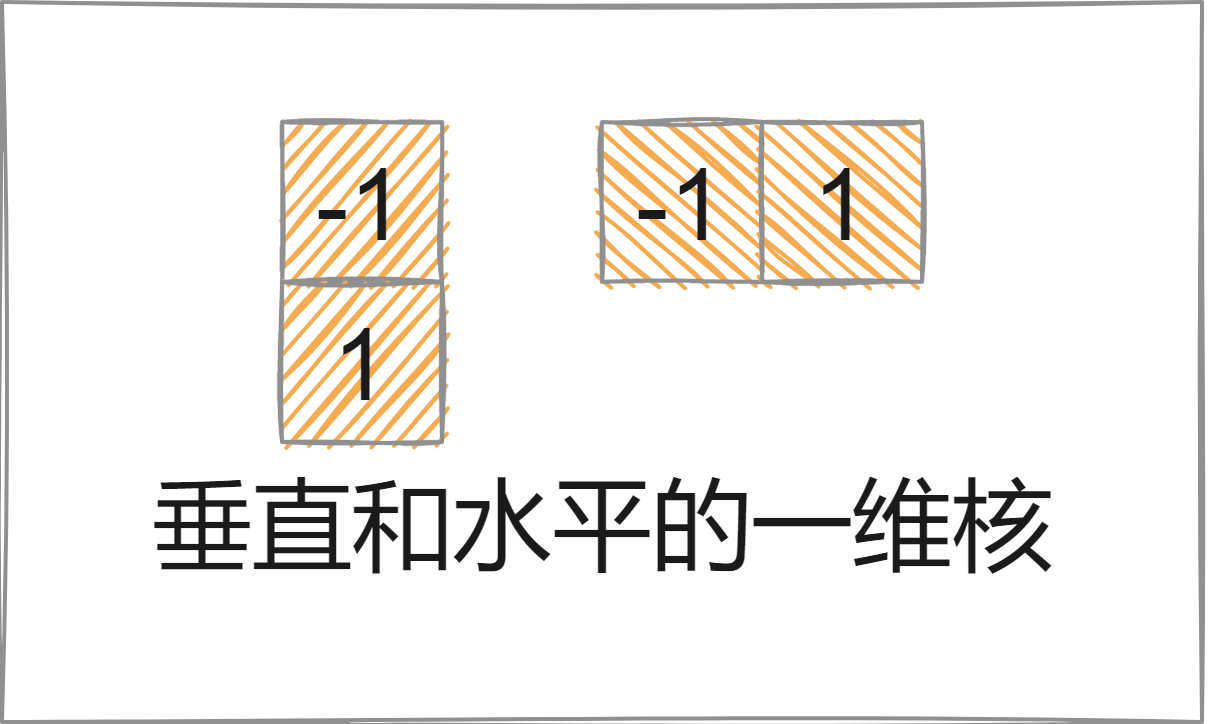
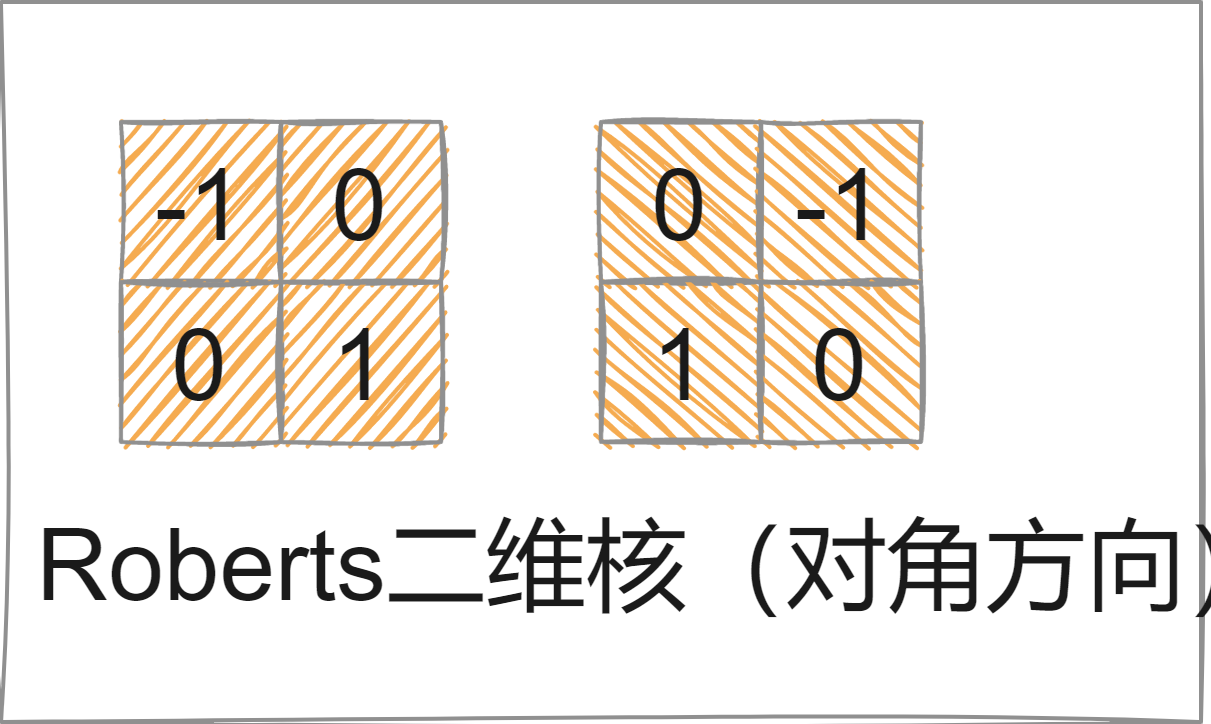
  1. 前向差分：有一维核也有二维核（Roberts核）

gx(x,y)=∂f(x,y)∂x=f(x+1,y)−f(x,y)g_x(x,y)=\frac{\partial f(x,y)} {\partial x}=f(x+1,y)-f(x,y)

gy(x,y)=∂f(x,y)∂y=f(x,y+1)−f(x,y)g_y(x,y)=\frac{\partial f(x,y)} {\partial y}=f(x,y+1)-f(x,y)

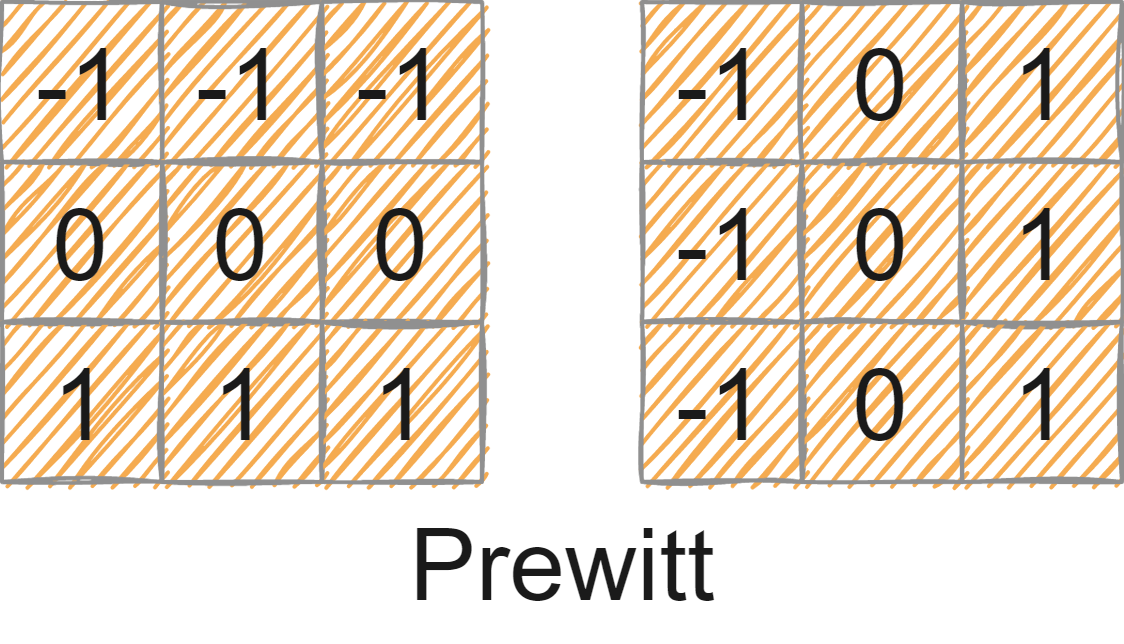
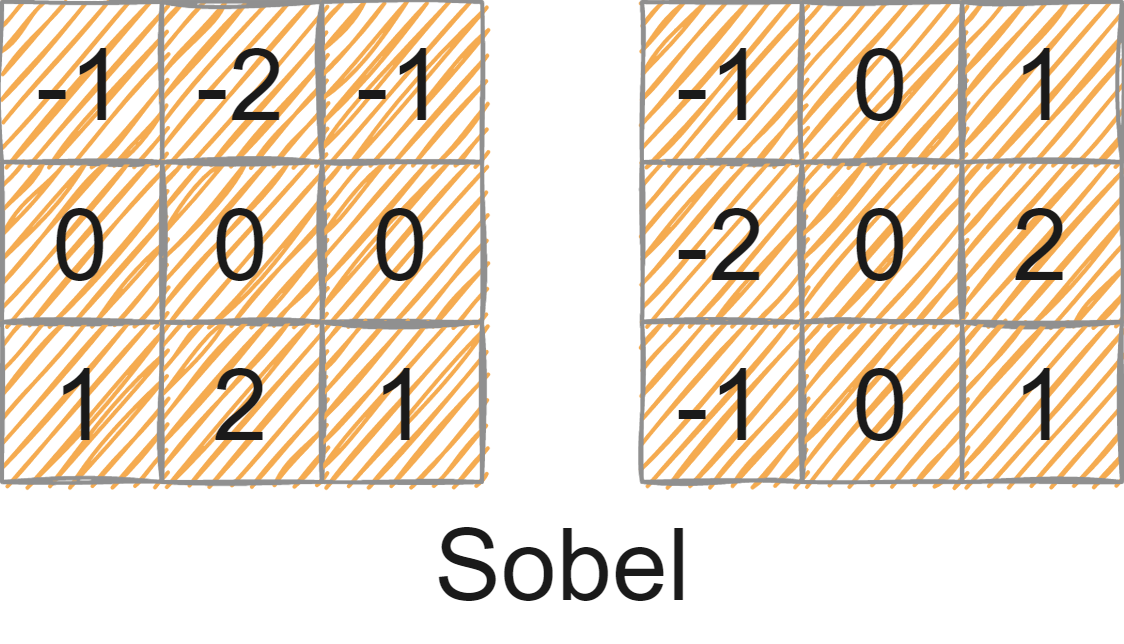
  1. 中心有限差分：常见有Prewitt核核Sobel核

点检测

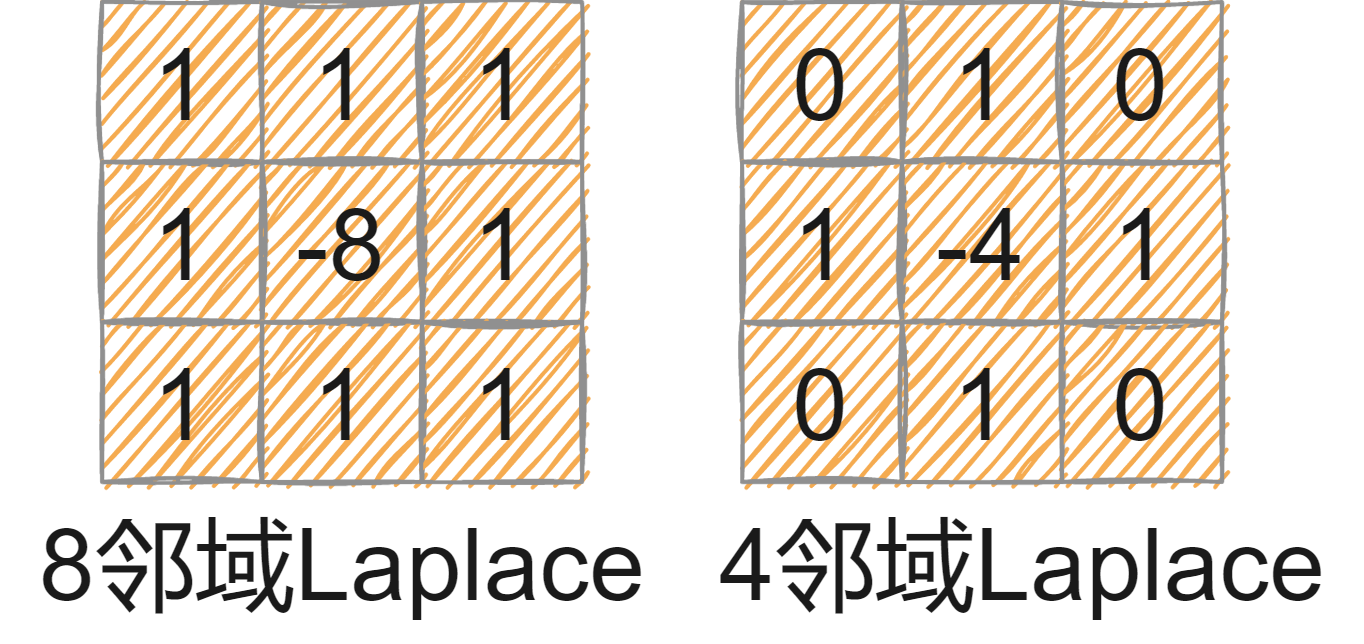
使用拉普拉斯核进行孤立点检测。

线检测

同样可以使用拉普拉斯核进行线检测，但也有规定方向的线检测。

边缘检测

部分代码如下：

1
2
3
4
5
6
7
8
9
10
cv::Mat kernel1 = (cv::Mat_<float>(2, 2) << -1, 0, 0, 1 );
cv::Mat kernel2 = (cv::Mat_<float>(2, 2) << 0, -1, 1, 0 );

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2

cv::convertScaleAbs(dst1, dst1);    // 取绝对值
cv::convertScaleAbs(dst2, dst2);    // 取绝对值

dst = dst1 + dst2;  // 合并

Prewitt边缘检测

部分代码如下：

1
2
3
4
5
6
7
8
9
10
cv::Mat kernel1 = (cv::Mat_<float>(3, 3) << -1, -1, -1, 0, 0, 0, 1, 1, 1);
cv::Mat kernel2 = (cv::Mat_<float>(3, 3) << -1, 0, 1, -1, 0, 1, -1, 0, 1);

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2

cv::convertScaleAbs(dst1, dst1);    // 取绝对值
cv::convertScaleAbs(dst2, dst2);    // 取绝对值

dst = dst1 + dst2;  // 合并

Sobel边缘检测

部分代码如下：

1
2
3
4
5
6
7
8
9
10
cv::Mat kernel1 = (cv::Mat_<float>(3, 3) << -1, -2, -1, 0, 0, 0, 1, 2, 1);
cv::Mat kernel2 = (cv::Mat_<float>(3, 3) << -1, 0, 1, -2, 0, 2, -1, 0, 1);

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2

cv::convertScaleAbs(dst1, dst1);    // 取绝对值
cv::convertScaleAbs(dst2, dst2);    // 取绝对值

dst = dst1 + dst2;  // 合并

Kirsch边缘检测

部分代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
cv::Mat kernel1 = (cv::Mat_<float>(3, 3) << -3, -3, 5, -3, 0, 5, -3, -3, 5);
cv::Mat kernel2 = (cv::Mat_<float>(3, 3) << 5, -3, -3, 5, 0, -3, 5, -3, -3);
cv::Mat kernel3 = (cv::Mat_<float>(3, 3) << 5, 5, 5, -3, 0, -3, -3, -3, -3);
cv::Mat kernel4 = (cv::Mat_<float>(3, 3) << -3, -3, -3, -3, 0, -3, 5, 5, 5);
cv::Mat kernel5 = (cv::Mat_<float>(3, 3) << -3, 5, 5, -3, 0, 5, -3, -3, -3);
cv::Mat kernel6 = (cv::Mat_<float>(3, 3) << 5, 5, -3, 5, 0, -3, -3, -3, -3);
cv::Mat kernel7 = (cv::Mat_<float>(3, 3) << -3, -3, -3, -3, 0, 5, -3, 5, 5);
cv::Mat kernel8 = (cv::Mat_<float>(3, 3) << -3, -3, -3, 5, 0, -3, 5, 5, -3);

cv::filter2D(src, dst1, -1, kernel1);    // 方向1
cv::filter2D(src, dst2, -1, kernel2);    // 方向2
cv::filter2D(src, dst3, -1, kernel3);    // 方向3
cv::filter2D(src, dst4, -1, kernel4);    // 方向4
cv::filter2D(src, dst5, -1, kernel5);    // 方向5
cv::filter2D(src, dst6, -1, kernel6);    // 方向6
cv::filter2D(src, dst7, -1, kernel7);    // 方向7
cv::filter2D(src, dst8, -1, kernel8);    // 方向8

cv::convertScaleAbs(dst1, dst1);
cv::convertScaleAbs(dst2, dst2);
cv::convertScaleAbs(dst3, dst3);
cv::convertScaleAbs(dst4, dst4);
cv::convertScaleAbs(dst5, dst5);
cv::convertScaleAbs(dst6, dst6);
cv::convertScaleAbs(dst7, dst7);
cv::convertScaleAbs(dst8, dst8);

dst = src.clone();
for (int i = 0; i < src.rows; i++)
    for (int j = 0; j < src.cols; j++)
    {
        int arr[] = { dst1.at<uchar>(i, j), dst2.at<uchar>(i, j)
            , dst3.at<uchar>(i, j), dst4.at<uchar>(i, j), dst5.at<uchar>(i, j)
            , dst6.at<uchar>(i, j), dst7.at<uchar>(i, j), dst8.at<uchar>(i, j) };
        std::sort(arr, arr + 8);
        int max_num = arr[7];
        dst.at<uchar>(i, j) = max_num;  // 取8个方向的最大值作为结果
    }

LOG边缘检测

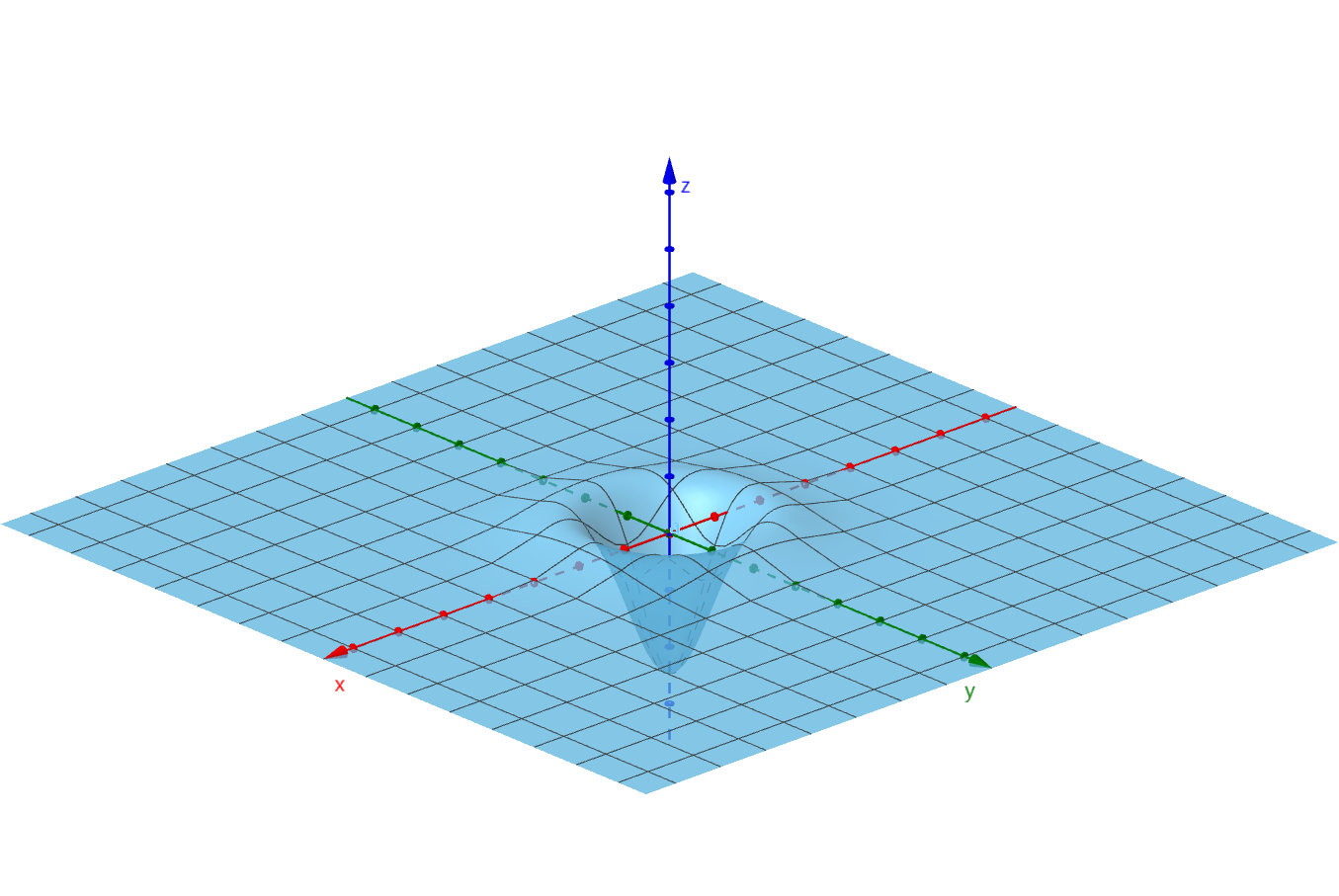
高斯拉普拉斯LOG函数：

∇2G(x,y)=(x2+y2−2σ2σ4)e−x2+y22σ2\nabla^2G(x,y)=(\frac{x^2+y^2-2\sigma^2} {\sigma^4})e^{-\frac{x^2+y^2} {2\sigma^2} }

其由拉普拉斯算子核高斯函数组成：

Laplacian:∇2f=∂2f∂x2+∂2f∂y2Laplacian: \nabla^2f=\frac{\partial^2f} {\partial x^2} + \frac{\partial^2f} {\partial y^2}

GaussianFunction:G(x,y)=e−x2+y22σ2Gaussian Function: G(x,y)=e^{-\frac{x^2+y^2} {2\sigma^2} }

∇2G(x,y)=∂2G(x,y)∂x2+∂2G(x,y)∂y2\nabla^2G(x,y)=\frac{\partial^2G(x,y)} {\partial x^2} + \frac{\partial^2G(x,y)} {\partial y^2}

构建LOG核的方法有两种：

  1. 由LOG函数进行计算（取样后要标定系数使系数和为0）；

  2. 构建高斯核，接着用拉普拉斯核进行卷积得到LOG核。

由于拉普拉斯和高斯是线性运算，使用LOG对图像进行边缘检测也有两种方法：

  1. 直接用LOG核对图像进行卷积。

g(x,y)=[∇2G(x,y)]⋆f(x,y)g(x,y)=[\nabla^2G(x,y)]\star f(x,y)

  1. 先对图像进行高斯滤波，再对滤波后图像进行拉普拉斯变换。

g(x,y)=∇2[G(x,y)⋆f(x,y)]g(x,y)=\nabla^2[G(x,y)\star f(x,y)]

代码如下：

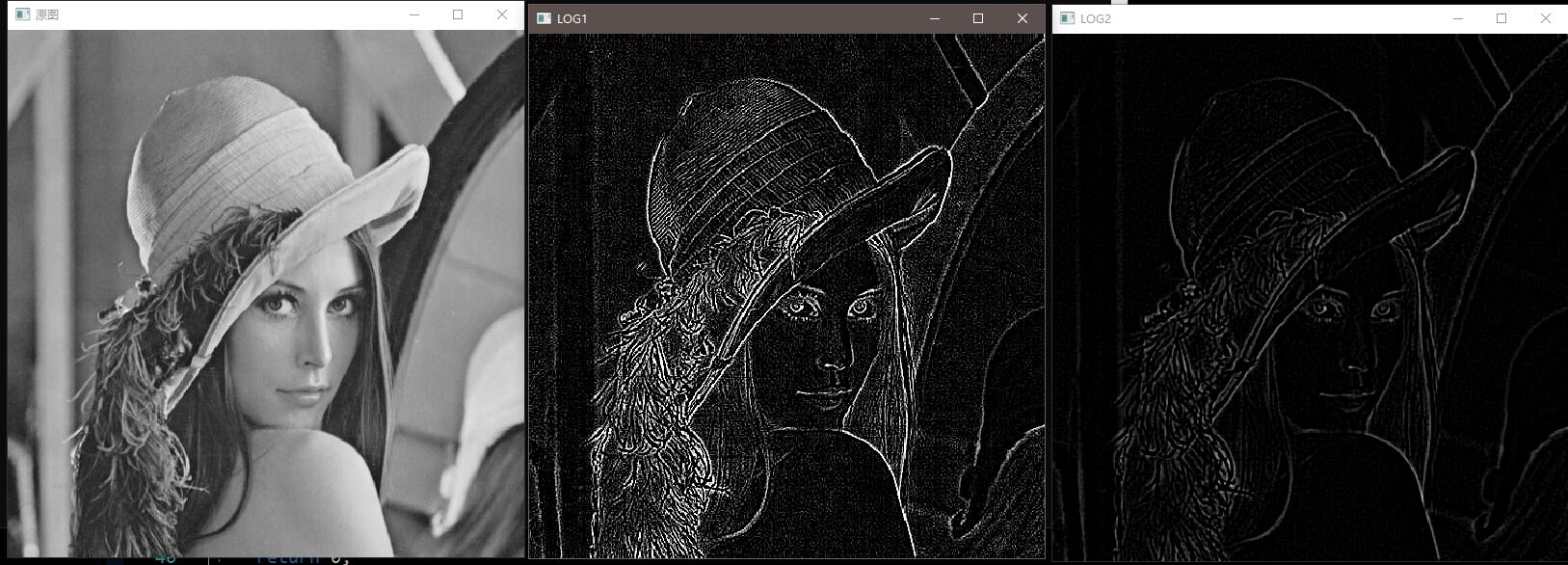
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <opencv2/opencv.hpp>

void LOG1(cv::Mat input, cv::Mat &output)
{
    output = input.clone();
    cv::Mat kernel = (cv::Mat_<float>(5, 5) <<
        0, 0, 1, 0, 0,
        0, 1, 2, 1, 0,
        1, 2, -16, 2, 1,
        0, 1, 2, 1, 0,
        0, 0, 1, 0, 0); // LOG核
    cv::filter2D(input, output, -1, kernel);
}

void LOG2(cv::Mat input, cv::Mat &output)
{
    output = input.clone();
    cv::GaussianBlur(input, output, cv::Size(5, 5), 1, 1);
    cv::Laplacian(output, output, input.depth(), 3, 1, 0, cv::BORDER_DEFAULT);
}

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1, dst2;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    LOG1(src, dst1);
    LOG2(src, dst2);

    cv::namedWindow("原图", cv::WINDOW_NORMAL);
    cv::namedWindow("LOG1", cv::WINDOW_NORMAL);
    cv::namedWindow("LOG2", cv::WINDOW_NORMAL);
    cv::imshow("原图", src);
    cv::imshow("LOG1", dst1);
    cv::imshow("LOG2", dst2);

    cv::waitKey(0);
    return 0;
}

效果截图：

Canny边缘检测

Canny检测是传统边缘检测算子中最优秀的，基于：

  1. 低错误率。所有边缘都应该找到，没有虚假边缘。

  2. 准确的定位边缘。检测到的边缘是接近真实的边缘。

  3. 单个边缘点响应。只返回单点厚度的结果。

Canny边缘检测的步骤

  1. 使用高斯滤波器平滑图像
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
void Gaussfilter(cv::Mat input, cv::Mat &output, int size, double sigma)
{
    // 处理核大小
    if (size < 3) size = 3;
    else size = static_cast<int>((size / 2) * 2 + 1);

    // 创建高斯核
    double **Gausskernel = new double *[size];
    for (int i = 0; i < size; i ++)
        Gausskernel[i] = new double[size];
    int center = size / 2;
    double sum = 0;

    for (int i = 0; i < size; i ++)
        for (int j = 0; j < size; j ++)
        {
            Gausskernel[i][j] = exp(-((i - center) * (i - center) + (j - center) * (j - center)) / (2 * sigma * sigma));
            sum += Gausskernel[i][j];
        }

    sum = 1.0 / sum;

    for (int i = 0; i < size; i ++)
        for (int j = 0; j < size; j ++)
            Gausskernel[i][j] *= sum;

    // 高斯滤波
    output = input.clone();
    for (int i = center; i < input.rows - center; i ++)
        for (int j = center; j < input.cols - center; j ++)
        {
            double sum = 0;
            for (int x = -center; x <= center; x ++)
                for (int y = -center; y <= center; y ++)
                    sum += Gausskernel[x + center][y + center] * input.at<uchar>(i + x, j + y);
            output.at<uchar>(i, j) = sum;
        }

    // 释放空间
    for (int i = 0; i < size; i ++) delete[] Gausskernel[i];
    delete[] Gausskernel;
}
  1. 计算梯度幅值和边缘方向

使用Prewitt算子计算梯度。

计算梯度也有两种方式：

G=Gx2+Gy2G=\sqrt{G_x^2+G_y^2}

G=Gx+GyG=G_x+G_y

根据边缘方向的法线方向确定边缘方向：

α(x,y)=arctan⁡[Gy(x,y)Gx(x,y)]\alpha(x,y)=\arctan\Big[\frac{G_y(x,y)} {G_x(x,y)}\Big]

然后根据法线方向将边缘分为四个方向：水平、垂直、45°、-45°。有：

  • 当法线方向为-22.5°~22.5°，或-157.5°~157.5°，则认为边缘为水平边缘；

  • 当法线方向为22.5°~67.5°，或-112.5°~-157.5°，则认为边缘为-45°边缘；

  • 当法线方向为67.5°~112.5°，或-67.5°~-112.5°，则认为边缘为垂直边缘；

  • 当法线方向为112.5°~157.5°，或-22.5°~-67.5°，则认为边缘为45°边缘；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
void GradDire(cv::Mat input, cv::Mat &Gradimg, cv::Mat &Direimg)
{
    Gradimg = cv::Mat(input.size(), CV_16U, cv::Scalar(0));
    Direimg = cv::Mat(input.size(), CV_8U, cv::Scalar(0));

    for (int i = 1; i < input.rows - 1; i++)
        for (int j = 1; j < input.cols - 1; j++)
        {
            // 计算梯度及梯度幅值
            int gx = input.at<uchar>(i + 1, j - 1) + input.at<uchar>(i + 1, j) + input.at<uchar>(i + 1, j + 1)
                - input.at<uchar>(i - 1, j - 1) - input.at<uchar>(i - 1, j) - input.at<uchar>(i - 1, j + 1);
            int gy = input.at<uchar>(i - 1, j + 1) + input.at<uchar>(i, j + 1) + input.at<uchar>(i + 1, j + 1)
                - input.at<uchar>(i - 1, j - 1) - input.at<uchar>(i, j - 1) - input.at<uchar>(i + 1, j - 1);
            int sum = gx + gy;
            Gradimg.at<ushort>(i, j) = std::abs(sum);

            // 方向图像，图像中的坐标轴，1-水平，2-45°，3-垂直，4--45°
            double dire = atan2(gy, gx) * 180 / 3.1415926;
            if (dire <= -67.5 or dire > 67.5)    Direimg.at<uchar>(i, j) = 1;
            else if (dire > -67.5 and dire < -22.5) Direimg.at<uchar>(i, j) = 2;
            else if (dire > -22.5 and dire < 22.5)    Direimg.at<uchar>(i, j) = 3;
            else Direimg.at<uchar>(i, j) = 4;
        }
}
  1. 非极大值抑制

非极大值抑制原理为：在一个3*3的邻域内，根据边缘法线方向，与法线方向上其他两个邻点的梯度幅值比较大小，若该点大于另外两个邻点，则认为该点是边缘点，否则抑制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
void NonMaxSuppression(cv::Mat Gradimg, cv::Mat Direimg, cv::Mat &Suppimg)
{
    Suppimg = cv::Mat(Gradimg.size(), Gradimg.type(), cv::Scalar(0));

    for (int i = 1; i < Gradimg.rows - 1; i++)
        for (int j = 1; j < Gradimg.cols - 1; j++)
        {
            switch (Direimg.at<uchar>(i, j))
            {
                case 1:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i, j - 1) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i, j + 1))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                case 2:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i + 1, j - 1) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i - 1, j + 1))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                case 3:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i - 1, j) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i + 1, j))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                case 4:
                    if (Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i - 1, j - 1) && Gradimg.at<ushort>(i, j) >= Gradimg.at<ushort>(i + 1, j + 1))
                        Suppimg.at<ushort>(i, j) = Gradimg.at<ushort>(i, j);
                    else
                        Suppimg.at<ushort>(i, j) = 0;
                    break;
                default:
                    break;
            }
        }
}
  1. 使用双阈值处理和连通性分析检测和链接边缘

只设置一个阈值时，若阈值设置太低，则会出现假边缘；若阈值设置太高，则一些弱边缘会被丢弃。

步骤：

  1. 设置两个阈值：高阈值Th和低阈值Tl，一般高比低为2:1到3:1。

  2. 分别用这两个阈值对非极大值抑制图像进行阈值处理得到二值图像BWh和BWl，其中BWl的非零像素包含BWh。

  3. 分为强边缘图像和弱边缘图像，令BWl = BWh - BWl。此时认为BWh为强边缘图像，BWl为弱边缘图像。

  4. 标记弱边缘图像的真实边缘：在BWh中定位下一个没有被访问过的边缘像素P；在BWl中，认为P点坐标的8邻域内的弱边缘像素为真实边缘病标记；若BWh中所有像素均被访问，则结束，否则继续标记。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void doubleThread(cv::Mat Suppimg, cv::Mat &Edgeimg, int Tl, int Th)
{
    if (Th < Tl)
        std::swap(Th, Tl);

    cv::Mat bw_h = cv::Mat(Suppimg.size(), CV_8UC1, cv::Scalar(0));
    cv::Mat bw_l = cv::Mat(Suppimg.size(), CV_8UC1, cv::Scalar(0));

    for (int i = 0; i < Suppimg.rows; i++)
        for (int j = 0; j < Suppimg.cols; j++)
        {
            if (Suppimg.at<ushort>(i, j) >= Th)
                bw_h.at<uchar>(i, j) = 255;
            else
                bw_h.at<uchar>(i, j) = 0;

            if (Suppimg.at<ushort>(i, j) >= Tl and Suppimg.at<ushort>(i, j) < Th)
                bw_l.at<uchar>(i, j) = 255;
            else
                bw_l.at<uchar>(i, j) = 0;
        }

    Edgeimg = bw_h.clone();
    for (int i = 1; i < Suppimg.rows - 1; i++)
        for (int j = 1; j < Suppimg.cols - 1; j++)
            if (bw_h.at<uchar>(i, j) == 255)
            {
                if (bw_l.at<uchar>(i - 1, j - 1) == 255)
                    Edgeimg.at<uchar>(i - 1, j - 1) = 255;
                if (bw_l.at<uchar>(i - 1, j) == 255)
                    Edgeimg.at<uchar>(i - 1, j) = 255;
                if (bw_l.at<uchar>(i - 1, j + 1) == 255)
                    Edgeimg.at<uchar>(i - 1, j + 1) = 255;
                if (bw_l.at<uchar>(i, j - 1) == 255)
                    Edgeimg.at<uchar>(i, j - 1) = 255;
                if (bw_l.at<uchar>(i, j + 1) == 255)
                    Edgeimg.at<uchar>(i, j + 1) = 255;
                if (bw_l.at<uchar>(i + 1, j - 1) == 255)
                    Edgeimg.at<uchar>(i + 1, j - 1) = 255;
                if (bw_l.at<uchar>(i + 1, j) == 255)
                    Edgeimg.at<uchar>(i + 1, j) = 255;
                if (bw_l.at<uchar>(i + 1, j + 1) == 255)
                    Edgeimg.at<uchar>(i + 1, j + 1) = 255;
            }
}

Canny函数

手搓的Canny函数：

1
2
3
4
5
6
7
8
9
void Canny_Edge(cv::Mat input, cv::Mat &output, int th, int tl, int size, double sigma)
{
    cv::Mat Gaussimg, Gradimg, Direimg, Suppimg, Edgeimg;
    Gaussfilter(input, Gaussimg, size, sigma);
    GradDire(Gaussimg, Gradimg, Direimg);
    NonMaxSuppression(Gradimg, Direimg, Suppimg);
    doubleThread(Suppimg, Edgeimg, tl, th);
    output = Edgeimg;
}

OpenCV自带的Canny函数；

1
void Canny(InputArray image, OutputArray edges, double threshold1, double threshold2, int apertureSize = 3, bool L2gradient = false);

参数；

  • image：8比特输入图像。

  • edges：输出边缘图，单通道8位图像，与图像大小相同。

  • threshold1：滞后过程的第一个阈值。

  • threshold2：滞后过程的第二个阈值。

  • apertureSize：Sobel算子大小。

  • L2gradient：计算图像梯度复制的标识。

效果截图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1, dst2;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    Canny_Edge(src, dst1, 50, 20, 3, 1);
    cv::Canny(src, dst2, 50, 20, 3, 1);

    cv::namedWindow("手搓Canny", cv::WINDOW_NORMAL);
    cv::namedWindow("Canny函数", cv::WINDOW_NORMAL);
    cv::imshow("手搓Canny", dst1);
    cv::imshow("Canny函数", dst2);
    cv::waitKey(0);
    return 0;
}

图像阈值分割

图像分割都是基于图像像素的灰度值，通过一个阈值T将图像中的像素分为两类或多类。

阈值分割的基本原理：

g(x,y)={1,if f(x,y)>T0,if f(x,y)≤Tg(x,y)=\begin{cases} 1,\quad if\ f(x,y)>T\\ 0, \quad if\ f(x,y)\leq T \end{cases}

一般的图像阈值分割方法都主要在于去通过图像自身信息去计算寻找合适的阈值。

全局阈值分割

迭代阈值分割

计算步骤：

  1. 为全局阈值T选择一个初始的估计值，一般是图像平均灰度值。

  2. 使用初始值T进行阈值分割，此时图像分为大于阈值的像素组G1和小于阈值的像素组G2；

  3. 分别计算属于G1、G2图像像素的平均灰度值m1和m2；

  4. 针对m1和m2计算一个新的阈值 T=m1+m22T=\frac{m1 + m2} {2} ；

  5. 重复2到4，直到连续迭代中计算的连续两个T的差小于某个预定义的值为止。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <opencv2/opencv.hpp>

void imageIterativeThresholdSegmentation(cv::Mat input, cv::Mat &output)
{
    cv::Mat src = input.clone();

    if (src.channels() == 3)    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);
    double T = 0, preT = 0;

    for (int i = 0; i < src.rows; i ++)
        for (int j = 0; j < src.cols; j ++)
            T += src.at<uchar>(i, j);

    T = 1.0 * T / (src.rows * src.cols);

    while (std::abs(preT - T) > 0.5)
    {
        preT = T;
        int mean1 = 0, mean2 = 0, cnt1 = 0, cnt2 = 0;
        for (int i = 0; i < src.rows; i ++)
            for (int j = 0; j < src.cols; j ++)
            {
                if (src.at<uchar>(i, j) > T)
                    mean1 += src.at<uchar>(i, j), cnt1 ++;
                else
                    mean2 += src.at<uchar>(i, j), cnt2 ++;
            }

        mean1 = 1.0 * mean1 / cnt1;
        mean2 = 1.0 * mean2 / cnt2;
        T = (mean1 + mean2) / 2;
    }

    cv::threshold(src, output, T, 255, cv::THRESH_BINARY);
}

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    imageIterativeThresholdSegmentation(src, dst1);

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst1", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst1", dst1);

    cv::waitKey(0);
    return 0;
}

效果截图：

OTSU大津法阈值分割

计算步骤：

  1. 计算图像灰度直方图的零阶累积距（累加直方图）：

zeroCumuMoment(k)=∑i=1khistogram(i),k∈[0,255]zeroCumuMoment(k)=\sum_{i=1}^khistogram(i),k\in[0,255]

  1. 计算灰度直方图的一阶累积距：

oneCumuMoment(k)=∑i=1k(i∗histogram(i)),k∈[0,255]oneCumuMoment(k)=\sum_{i=1}^k(i*histogram(i)),k\in[0,255]

  1. 计算输入图像的总体灰度平均值mean，也就是k=255时的一阶累积距：

mean=oneCumuMoment(255)mean=oneCumuMoment(255)

  1. 计算每一个灰度级作为阈值时，前景区域的平均灰度、背景区域的平均灰度与整体图像平均灰度的方差，方差计算：

σ2(k)=(mean∗zeroCumuMoment(k)−oneCumuMoment(k))2zeroCumuMoment(k)∗(1−zeroCumuMoment(k)),k∈[0,255]\sigma^2(k)=\frac{(mean*zeroCumuMoment(k)-oneCumuMoment(k))^2} {zeroCumuMoment(k)*(1-zeroCumuMoment(k))},k\in[0,255]

  1. 找到最大的 σ2(k)\sigma^2(k) ，即是所求的阈值：

thresh=max⁡(σ2(k)),k∈[0,255]thresh=\max(\sigma^2(k)),k\in[0,255]

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <opencv2/opencv.hpp>

void imageotsuThresholdSegmentation(cv::Mat input, cv::Mat &output)
{
    cv::Mat src = input.clone();

    if (src.channels() == 3)    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    // 计数灰度直方图各像素值
    int hist[256] = { 0 };
    for (int i = 0; i < src.rows; i ++)
        for (int j = 0; j < src.cols; j ++)
            hist[src.at<uchar>(i, j)] ++;

    // 计算灰度直方图各像素概率
    double phist[256] = { 0 };
    for (int i = 0; i < 256; i ++)
        phist[i] = 1.0 * hist[i] / (src.rows * src.cols);

    double zeroCumuMoment[256] = { 0 }, oneCumuMoment[256] = { 0 };

    // 计算灰度直方图的零阶累积距和一阶累积距
    zeroCumuMoment[0] = phist[0];
    oneCumuMoment[0] = 0 * phist[0];
    for (int i = 1; i < 256; i ++)
    {
        zeroCumuMoment[i] = zeroCumuMoment[i - 1] + phist[i];
        oneCumuMoment[i] = oneCumuMoment[i - 1] + i * phist[i];
    }

    double mean = oneCumuMoment[255];

    double _max = -1;
    int threshold = 0;

    for (int i = 0; i < 256; i ++)
    {
        double tmp = mean * zeroCumuMoment[i] - oneCumuMoment[i];
        double tmp1 = zeroCumuMoment[i] * (1 - zeroCumuMoment[i]);
        double ans = tmp * tmp / tmp1;
        if (_max < ans)
        {
            _max = ans;
            threshold = i;
        }
    }

    cv::threshold(src, output, threshold, 255, cv::THRESH_BINARY);
}

int main()
{
    cv::Mat src = cv::imread("src/lena.jpg");
    cv::Mat dst1;
    cv::cvtColor(src, src, cv::COLOR_BGR2GRAY);

    imageotsuThresholdSegmentation(src, dst1);

    cv::namedWindow("src", cv::WINDOW_NORMAL);
    cv::namedWindow("dst1", cv::WINDOW_NORMAL);
    cv::imshow("src", src);
    cv::imshow("dst1", dst1);

    cv::waitKey(0);
    return 0;
}

可变阈值处理

将图像划分为多个局部，对于每个局部都采取阈值分割，使得效果更好。

更多

  • 使用超像素分割图像

  • 使用图割分割区域

  • 使用形态学分水岭分割区域

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。