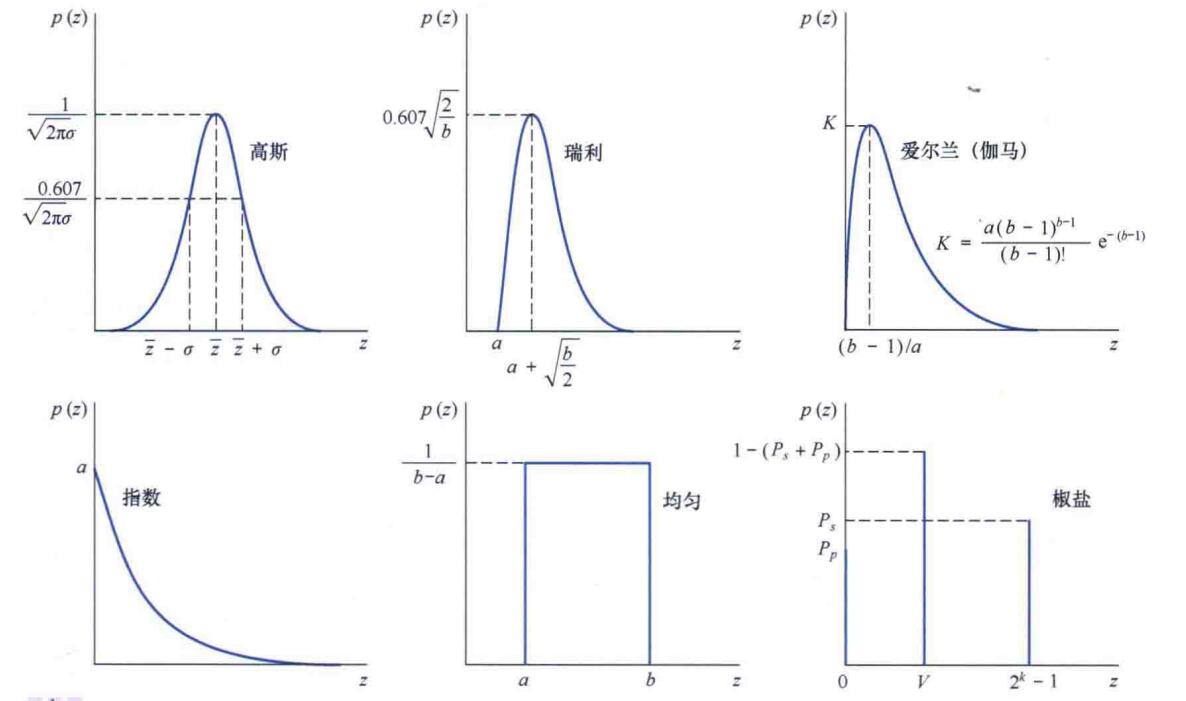
噪声分量的灰度值可视为随机变量，故讨论概率密度函数。

噪声模型

噪声模型概率密度函数

高斯噪声

概率密度函数（PDF，Probability Density Function）：

p(z)=12πσe−(z−z‾)2/2σ2,−∞<z<∞p(z)=\frac {1} {\sqrt{2\pi}\sigma}e^{-(z-\overline{z})^2/2\sigma^2},-\infty<z<\infty

其中， zz 表示灰度， z‾\overline{z} 表示 zz 的均值， σ\sigma 是 zz 的标准差。

瑞利噪声

PDF为：

p(z)={2b(z−a)e−(z−a)2/b,z≥a0,z<ap(z)=\begin{cases} \frac{2} {b}(z-a)e^{-(z-a)^2/b}&,z\geq a\\ 0&,z<a \end{cases}

当z由瑞利PDF表征时，均值为 z‾=a+πb/4\overline{z}=a+\sqrt{\pi b/4} ，方差为 σ2=b(4−π)4\sigma^2=\frac{b(4-\pi)} {4} 。

爱尔兰（伽马）噪声

PDF为：

p(z)={abzb−1(b−1)!e−az,z≥00,z<0p(z)=\begin{cases} \frac{a^bz^{b-1} } {(b-1)!}e^{-az}&,z\geq 0\\ 0&,z<0 \end{cases}

其中，a>b，z的均值为 z‾=ab\overline{z}=\frac{a} {b} ，方差为 σ2=ba2\sigma^2=\frac{b} {a^2}

指数噪声

PDF为：

p(z)={ae−az,z≥00,z<0p(z)=\begin{cases} ae^{-az}&,z\geq 0\\ 0&,z<0 \end{cases}

其中，a>0，z的均值为 z‾=1a\overline{z}=\frac{1} {a} ，方差为 σ2=1a2\sigma^2=\frac{1} {a^2} 。其为爱尔兰PDF在b=1时的特殊情况。

均匀噪声

PDF为：

p(z)={1b−a,a≤z≤b0,其他p(z)=\begin{cases} \frac{1} {b-a}&,a\leq z\leq b\\ 0&,其他 \end{cases}

其中，z的均值为 z‾=a+b2\overline{z}=\frac{a+b} {2} ，方差为 σ2=(b−a)212\sigma^2=\frac{(b-a)^2} {12}

椒盐噪声

PDF为：

p(z)={Ps,z=2k−1Pp,z=01−(Ps+Pp),z=Vp(z)=\begin{cases} P_s&,z=2^k-1\\ P_p&,z=0\\ 1-(P_s+P_p)&,z=V \end{cases}

其中，V是区间 0<V<2k−10<V<2^k-1 内的任意整数，k是数字图像中灰度值的比特数。像素被盐粒或胡椒噪声污染的概率P为 P=Ps+PpP=P_s+P_p 。P为噪声密度。

椒盐噪声的均值为 z‾=(0)Pp+K(1−Ps−Pp)+(2k−1)Ps\overline{z}=(0)P_p+K(1-P_s-P_p)+(2^k-1)P_s ，

方差为 σ2=(0−z‾)2Pp+(K−z‾)2(1−Ps−Pp)+(2k−1)Ps\sigma^2=(0-\overline{z})^2P_p+(K-\overline{z})^2(1-P_s-P_p)+(2^k-1)P_s 。

判别噪声类别

椒盐噪声可以肉眼区分。

其他噪声需要取图像中灰度较为平滑的区域，使用灰度分布图判断。

不同噪声区别

由上图可知，选取较为平滑的区域，高斯噪声后的直方图与高斯噪声PDF类似，而均匀噪声后的直方图与均匀噪声PDF类似。

上图代码实现

有关函数：

1
2
3
4
5
void fill(InputOutputArray mat,
		  int distType,
		  InputArray a,
		  InputArray b,
		  bool saturateRange = false);

该函数属于OpenCV 4的RNG类，是一个非静态成员函数，因此在使用的时候不能像使用正常函数一样的直接使用，而需要首先创建一个RNG类的变量，之后通过访问这个变量中函数进行调用这个函数。

该函数参数如下：

  • mat：用于存放随机数的矩阵，目前只支持低于5通道的矩阵。

  • distType：随机数分布形式选择标志，目前生成的随机数支持均匀分布（RNG::UNIFORM，0）和高斯分布（RNG::NORMAL，1）。

  • a：确定分布规律的参数。当选择均匀分布时，该参数表示均匀分布的最小下限；当选择高斯分布时，该参数表示高斯分布的均值。

  • b：确定分布规律的参数。当选择均匀分布时，该参数表示均匀分布的最大上限；当选择高斯分布时，该参数表示高斯分布的标准差。

  • saturateRange：预饱和标志，仅用于均匀分布。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <opencv2/opencv.hpp>

// 添加高斯噪声
void GaussianNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::NORMAL, 10, 50);    // 使用NORMAL参数添加高斯噪声
    output = input + noice;
}

// 添加均匀噪声
void UniformNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::UNIFORM, 10, 50);    // 使用UNIFORM参数添加高斯噪声
    output = input + noice;
}

void getHist(cv::Mat& input, cv::Mat& histImage)
{
    // 划出感兴趣区域
    cv::Mat ioa(cv::Mat::zeros(input.size(), CV_8U));
    for (int i = 0; i < 100; i ++)
        for (int j = 900; j < 1000; j ++)
            ioa.at<uchar>(i, j) = 255;
    // 框出感兴趣区域
    cv::rectangle(input, cv::Rect(900, 0, 100, 100), cv::Scalar(0, 0, 255), 5);

    /* ————————计算并绘制直方图———————— */
    cv::Mat hist;
    int hsize = 256;    // 直方图区间数
    float ranges[] = { 0, 256 };   // 统计像素值的区间
    const float *hRanges = { ranges };
    // 计算直方图的输出值
    cv::calcHist(&input, 1, 0, ioa, hist, 1, &hsize, &hRanges, true, false);

    int hist_h = 300, hist_w = 512; // 直方图图像高和宽
    int bin_w = hist_w / hsize; // 区间

    // 直方图图像
    histImage = cv::Mat(hist_h, hist_w, CV_8UC3, cv::Scalar(255, 255, 255));
    // 直方图输出值归一化到0~255
    cv::normalize(hist, hist, 0, hist_h, cv::NORM_MINMAX, -1, cv::Mat());

    for (int i = 1; i < hsize; i ++)
        cv::line(histImage, cv::Point((i - 1) * bin_w, hist_h - cvRound(hist.at<float>(i - 1))), cv::Point((i) *bin_w, hist_h - cvRound(hist.at<float>(i))), cv::Scalar(100, 100, 100), 2);
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2, hi1, hi2, hi;

    GaussianNoise(input, output1);
    UniformNoise(input, output2);
    getHist(input, hi);
    getHist(output1, hi1);
    getHist(output2, hi2);

    cv::namedWindow("原图", cv::WINDOW_NORMAL);
    cv::imshow("原图", input);
    cv::namedWindow("原图直方图", cv::WINDOW_NORMAL);
    cv::imshow("原图直方图", hi);
    cv::namedWindow("高斯噪声后图", cv::WINDOW_NORMAL);
    cv::imshow("高斯噪声后图", output1);
    cv::namedWindow("均匀噪声后图", cv::WINDOW_NORMAL);
    cv::imshow("均匀噪声后图", output2);
    cv::namedWindow("高斯噪声后直方图", cv::WINDOW_NORMAL);
    cv::imshow("高斯噪声后直方图", hi1);
    cv::namedWindow("均匀噪声后直方图", cv::WINDOW_NORMAL);
    cv::imshow("均匀噪声后直方图", hi2);

    cv::waitKey(0);

    return 0;
}

常见的空间滤波方法

均值滤波器

  • 算术均值滤波器：也是盒式滤波器，平滑图像中的局部变化，会降低噪声，也会模糊图像。

  • 几何均值滤波器：比算术均值滤波器相比丢失细节少。

  • 谐波平均滤波器：适合处理高斯噪声及盐粒噪声，但不能处理胡椒噪声。

  • 逆谐波均值滤波器：调节阶数有不同的效果。

统计排序滤波器

  • 中值滤波器：处理单极、双极冲激噪声更好，也能有效降低某些随机噪声，丢失细节更少。

  • 最大最小值滤波器：分别减少暗点和亮点，如胡椒噪声和盐粒噪声。可通过最大值滤波器削减胡椒噪声，通过最小值滤波器削减盐粒噪声。

  • 中点滤波器：适合处理随机分布的噪声，如高斯噪声和均匀噪声。

  • 修正阿尔法均值滤波器：适合处理多种混合噪声，如高斯噪声和椒盐噪声。

自适应滤波器

  • 自适应局部降噪滤波器：与均值滤波器比结果更清晰。

  • 自适应中值滤波器：平滑时保留图像细节。

均值滤波器

算术平均滤波器

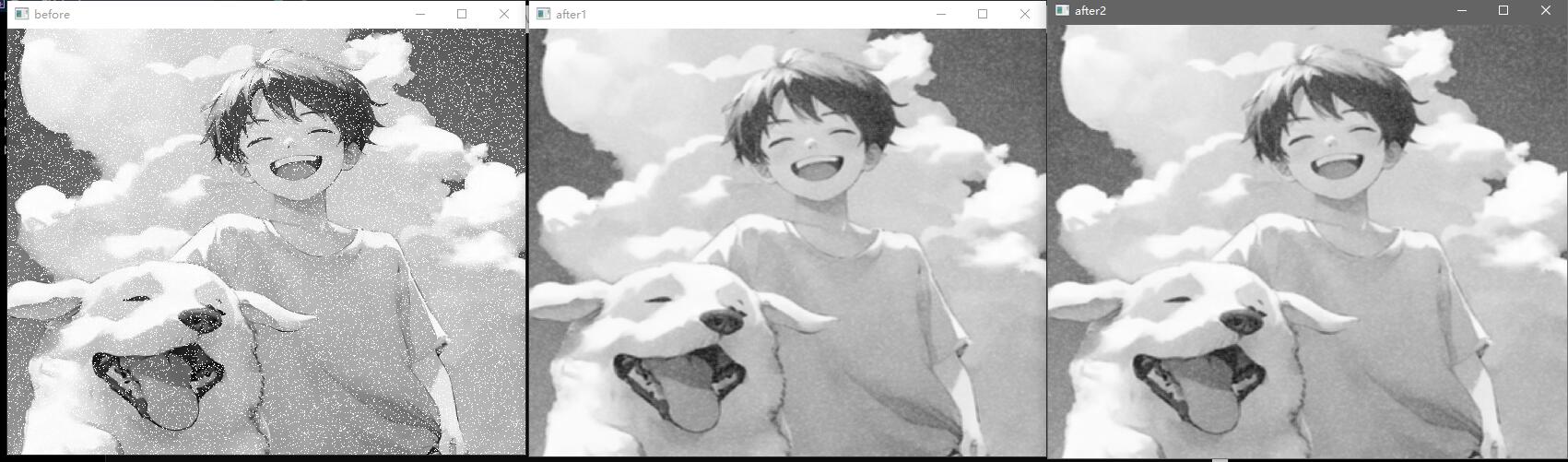
算术均值滤波器：也是盒式滤波器，平滑图像中的局部变化，会降低噪声，也会模糊图像。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=1mn∑(r,c)∈Sxyg(r,c)\hat f(x,y)=\frac{1} {mn}\sum_{(r,c)\in S_{xy} }g(r,c)

代码（Salt的相关代码见最后）：

相关函数：

1
void copyMakeBorder(InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar& value = Scalar())

该函数用于扩充图像边界，参数如下：

  • src：输入图像；

  • dst：输出与输入图像相同类型图像；

  • top、bottom、left、right：在图像的四个方向上扩充像素值；

  • borderType：边界类型。取值BORDER_CONSTANT为复制指定常量扩展边界；取值为BORDER_REPLICATE为自我复制扩展边界；取值为BORDER_REFLECT为通过镜像复制扩展边界；取值为BORDER_WRAP为复制对边像素扩展边界；

  • value：边界类型为BORDER_CONSTANT时表示边界值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void ArithmeticMeanFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int sum = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                    sum += input.at<uchar>(i + x, j + y);
            // 计算算术均值
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round(sum / (m * n));
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    ArithmeticMeanFilter(input, output1, 7, 7);
    // OpenCV盒式滤波器
    cv::blur(input, output2, cv::Size(7, 7));

    cv::namedWindow("after1", cv::WINDOW_NORMAL);
    cv::imshow("after1", output1);
    cv::namedWindow("after2", cv::WINDOW_NORMAL);
    cv::imshow("after2", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

算术平均滤波器效果

几何均值滤波器

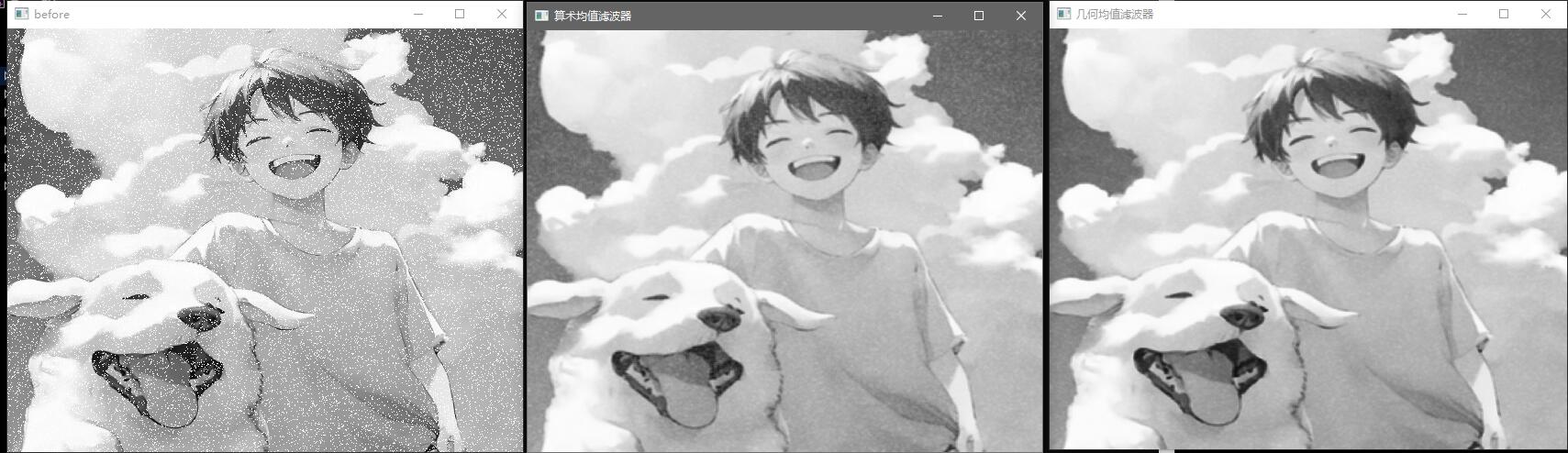
几何均值滤波器：比算术均值滤波器相比丢失细节少。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=[∏(r,c)∈Sxyg(r,c)]1mn\hat f(x,y)=\bigg[\prod_{(r,c)\in S_{xy} }g(r,c)\bigg]^{\frac {1} {mn} }

代码（Salt的相关代码见最后）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void GeometricMeanFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    double k = m * n;
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            double sum = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                    sum += log10(input.at<uchar>(i + x, j + y) + 0.1);
            // 使用对数进行运算指数，避免数值过大
            sum /= k;
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round(pow(10, sum));
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    GeometricMeanFilter(input, output1, 7, 7);
    // OpenCV盒式滤波器
    cv::blur(input, output2, cv::Size(7, 7));

    cv::namedWindow("几何均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("几何均值滤波器", output1);
    cv::namedWindow("算术均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("算术均值滤波器", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

算术均值滤波器和几何均值滤波器对比

谐波均值滤波器

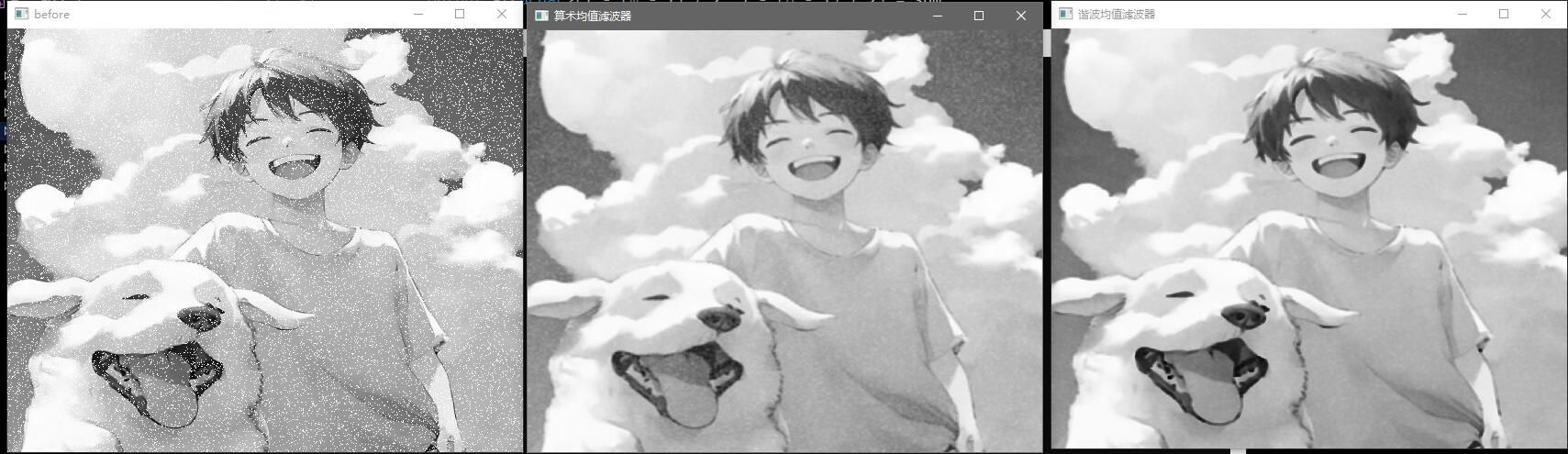
谐波平均滤波器：适合处理高斯噪声及盐粒噪声，但不能处理胡椒噪声。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=mn∑(r,c)∈Sxy1g(r,c)\hat f(x,y)=\frac{mn} {\sum_{(r,c)\in S_{xy} }\frac{1} {g(r,c)} }

代码（Salt的相关代码见最后）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void HarmonicMeanFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    double k = m * n;
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            double sum = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                    sum += 1.0 / (input.at<uchar>(i + x, j + y) + 0.1);
            sum = k / sum;
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = sum;
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    HarmonicMeanFilter(input, output1, 7, 7);
    // OpenCV盒式滤波器
    cv::blur(input, output2, cv::Size(7, 7));

    cv::namedWindow("谐波均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("谐波均值滤波器", output1);
    cv::namedWindow("算术均值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("算术均值滤波器", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

谐波均值滤波器和算术均值滤波器比较

反谐波均值滤波器

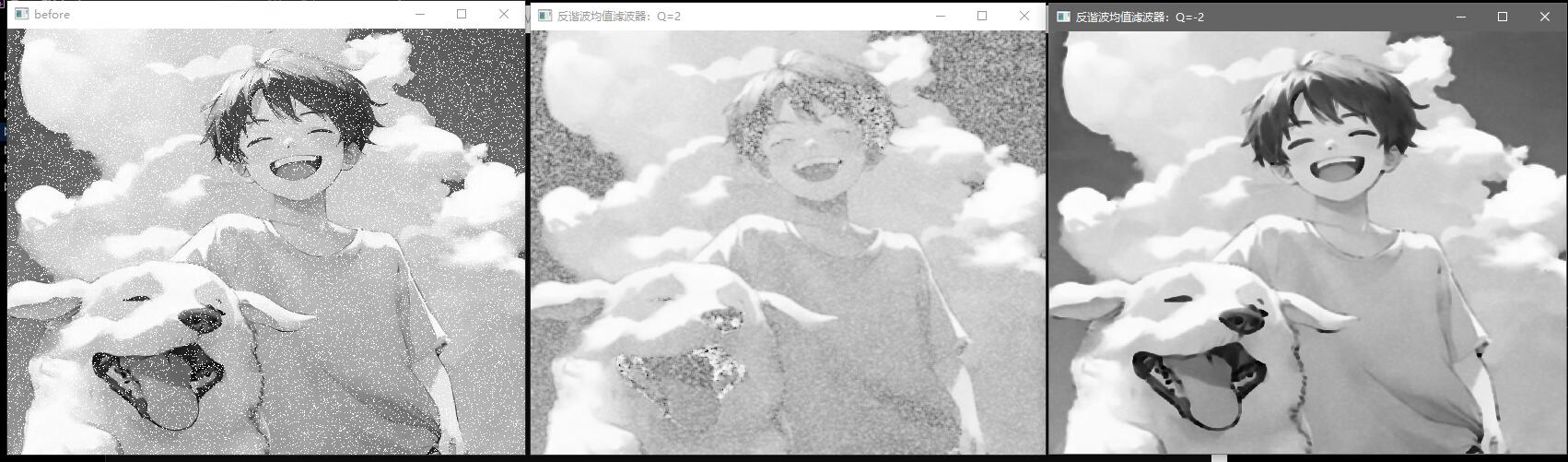
反谐波均值滤波器：调节阶数有不同的效果，适用于降低或消除椒盐噪声，当阶数Q为正时，可消除胡椒噪声；当阶数Q为负时，可消除盐粒噪声；Q=0时简化为算术平均滤波器；Q=-1时简化为谐波平均滤波器。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 表示中心为(x,y)、大小为m×n的矩形子图像窗口的一组坐标， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=∑(r,c)∈Sxyg(r,c)Q+1∑(r,c)∈Sxyg(r,c)Q\hat f(x,y)=\frac{\sum_{(r,c)\in S_{xy} }g(r,c)^{Q+1} } {\sum_{(r,c)\in S_{xy} }g(r,c)^Q}

代码（Salt的相关代码见最后）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void AntiharmonicAveragingFilter(cv::Mat input, cv::Mat &output, int m, int n, int q)
{
    output = input.clone();
    // 以镜像复制扩充边界
    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);


    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            double sum1 = 0, sum2 = 0, sum;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    sum1 += pow(input.at<uchar>(i + x, j + y), q + 1);
                    sum2 += pow(input.at<uchar>(i + x, j + y), q);
                }
            sum = sum1 / sum2;
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = cv::saturate_cast<uchar>(sum);
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现方法
    AntiharmonicAveragingFilter(input, output1, 7, 7, 2);
    AntiharmonicAveragingFilter(input, output2, 7, 7, -2);

    cv::namedWindow("反谐波均值滤波器：Q=2", cv::WINDOW_NORMAL);
    cv::imshow("反谐波均值滤波器：Q=2", output1);
    cv::namedWindow("反谐波均值滤波器：Q=-2", cv::WINDOW_NORMAL);
    cv::imshow("反谐波均值滤波器：Q=-2", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

反谐波均值滤波器

1
2
3
4
5
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, int n);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//Salt.cpp
#include "Salt.h"

void Salt(cv::Mat input, int n)
{
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            input.at<uchar>(i, j) = 255;
        else if (input.channels() == 3)
            input.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255);
    }
}

统计排序滤波器

中值滤波器

处理单极、双极冲激噪声更好，也能有效降低某些随机噪声，丢失细节更少。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 是中心为(x,y)的子图像， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=median(r,c)∈Sxy{g(r,c)}\hat f(x,y)=median_{(r,c)\in S_{xy} }\{g(r,c)\}

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MedianFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = arry[(num - 1) / 2];
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    // 自实现中值滤波器
    MedianFilter(input, output1, 7, 7);
    // OpenCV自带中值滤波器
    cv::medianBlur(input, output2, 7);

    cv::namedWindow("自实现中值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("自实现中值滤波器", output1);
    cv::namedWindow("OpenCV自带中值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("OpenCV自带中值滤波器", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

中值滤波器

最大值滤波器

滤波窗口的最大值作为滤波结果，可通过最大值滤波器削减胡椒噪声，也可削弱明色区域相邻的暗色区域。其中 f^\hat f 为复原的图像， SxyS_{xy} 是中心为(x,y)的子图像， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=max⁡(r,c)∈Sxy{g(r,c)}\hat f(x,y)=\max_{(r,c)\in S_{xy} }\{g(r,c)\}

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MaxFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = arry[num - 1];
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    Salt(input, 100000);    // 给图片添加10w个黑色噪点（胡椒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    MaxFilter(input, output, 7, 7);

    cv::namedWindow("最大值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("最大值滤波器", output);

    cv::waitKey(0);
    return 0;
}

效果展示：

最大值滤波器

最小值滤波器

滤波窗口的最小值作为滤波结果，可通过最小值滤波器削减盐粒噪声，也可削弱暗色区域相邻的明色区域。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 是中心为(x,y)的子图像， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=min⁡(r,c)∈Sxy{g(r,c)}\hat f(x,y)=\min_{(r,c)\in S_{xy} }\{g(r,c)\}

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MinFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = arry[0];
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    MinFilter(input, output, 7, 7);

    cv::namedWindow("最小值滤波器", cv::WINDOW_NORMAL);
    cv::imshow("最小值滤波器", output);

    cv::waitKey(0);
    return 0;
}

效果展示：

最小值滤波器

中点滤波器

滤波窗口的最大值和最小值的均值作为滤波结果，适合处理随机分布的噪声，如高斯噪声和均匀噪声。表达式如下，其中 f^\hat f 为复原的图像， SxyS_{xy} 是中心为(x,y)的子图像， g(x,y)g(x,y) 为被污染的图像：

f^(x,y)=12[max⁡(r,c)∈Sxy{g(r,c)}+min⁡(r,c)∈Sxy{g(r,c)}]\hat f(x,y)=\frac 12\bigg[\max_{(r,c)\in S_{xy} }\{g(r,c)\}+\min_{(r,c)\in S_{xy} }\{g(r,c)\}\bigg]

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void MidPointFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);
    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round((arry[0] + arry[num - 1]) / 2);
        }

}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    MidPointFilter(input, output, 7, 7);

    cv::namedWindow("中点滤波器", cv::WINDOW_NORMAL);
    cv::imshow("中点滤波器", output);

    cv::waitKey(0);
    return 0;
}

效果展示：

不太适合盐粒噪声

中值滤波器

修正阿尔法均值滤波器

假设要在邻域 SxyS_{xy} 内删除 g(r,c)g(r,c) 的 dd 个最低灰度值和 dd 个最高灰度值。令 g(r,c)g(r,c) 表示S中剩下的 mn−2dmn-2d 个像素，通过平均这些剩余像素所形成的滤波器，称为修正阿尔法均值滤波器。

当 d=0d=0 时简化为算术平均滤波器，当 d=(mn−1)/2d=(mn-1)/2 时变成中值滤波器，当 dd 为其他值时适合处理多种混合噪声，如高斯噪声和椒盐噪声。

f^(x,y)=1mn−2d∑(r,c)∈SxygR(r,c)\hat f(x,y)=\frac{1} {mn-2d}\sum_{(r,c)\in S_{xy} }g_R(r,c)

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

void ModifiedAlphaMeanFilter(cv::Mat input, cv::Mat &output, int m, int n, int d)
{
    output = input.clone();
    int num = m * n;
    std::vector<uchar> arry(num);

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x ++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry[h] = input.at<uchar>(i + x, j + y);
                    h += 1;
                }
            std::sort(arry.begin(), arry.end());
            int sum = 0;
            for (int k = d; k < num - d - 1; k ++)
                sum += arry[k];
            output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = round(sum / (num - 2 * d));
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    Salt(input, 100000);    // 给图片添加10w个白色噪点（盐粒噪声）

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    ModifiedAlphaMeanFilter(input, output1, 7, 7, 3);
    ModifiedAlphaMeanFilter(input, output2, 7, 7, 9);

    cv::namedWindow("修正阿尔法均值滤波器：d=3", cv::WINDOW_NORMAL);
    cv::imshow("修正阿尔法均值滤波器：d=3", output1);
    cv::namedWindow("修正阿尔法均值滤波器：d=9", cv::WINDOW_NORMAL);
    cv::imshow("修正阿尔法均值滤波器：d=9", output2);

    cv::waitKey(0);
    return 0;
}

效果展示：

修正阿尔法均值滤波器

1
2
3
4
5
6
//Salt.h
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, int n);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include "Salt.h"

void Salt(cv::Mat input, int n)
{
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            input.at<uchar>(i, j) = 255; //试验最大值滤波器时取为0
        else if (input.channels() == 3)
            input.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255); //试验最大值滤波器时取为(0,0,0)
    }
}

自适应滤波器

自适应局部降噪滤波器

滤波器对中心(x,y)的一个邻域 SxyS_{xy} 进行操作，

  • 噪声图像g(x,y)，噪声方差 ση2\sigma_\eta^2 ；

  • SxyS_{xy} 中像素的平均灰度 z‾Sxy\overline{z}_{S_{xy} } ， SxyS_{xy} 中像素灰度的局部方差 σSxy2\sigma^2_{S_{xy} } ；

希望滤波器满足：

  1. 噪声为0时，(x,y)处的值g等于f。若噪声图像方差 ση2=0\sigma^2_\eta=0 ，则滤波器仅返回(x,y)处的值g。

  2. 高局部方差通常与边缘相关，且应保留这些边缘。若局部方差 σSxy2\sigma^2_{S_{xy} } 与 ση2\sigma_\eta^2 高度相关，则滤波器返回(x,y)处一个接近于g的值。

  3. 当局部区域的性质与整个图像的性质相同时，则两个方差相等，滤波器返回 SxyS_{xy} 中像素的算术平均值，平均运算降低局部噪声。

处理步骤：

  1. 计算噪声图像方差 ση2\sigma^2_\eta ；

  2. 计算滤波器窗口内像素的均值 zSsyz_{S_{sy} } 和方差 σSxy2\sigma^2_{S_{xy} } ；

  3. 利用下式计算：

f^(x,y)=g(x,y)−ση2σSxy2[g(x,y)−zSxy‾],ση2σSxy2≤1\hat{f}(x,y)=g(x,y)-\frac{\sigma^2_{\eta} } {\sigma^2_{S_{xy} }}\big[g(x,y)-\overline{z_{S_{xy} }}\big],\frac{\sigma^2_{\eta} } {\sigma^2_{S_{xy} }}\leq1

代码：

涉及OpenCV函数：

1
void meanStdDev(InputArray src, OutputArray mean, OutputArray stddev, InputArray mask=noArray());

参数分别为：

  • src：输入矩阵

  • mean：输出均值

  • stddev：输出标准差

  • mask：可选参数，掩码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
#include <opencv2/opencv.hpp>

// 添加高斯噪声
void GaussianNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::NORMAL, 10, 20);    // 使用NORMAL参数添加高斯噪声
    output = input + noice;
}

void AdaptiveLocalNoiseReductionFilter(cv::Mat input, cv::Mat &output, int m, int n)
{
    output = input.clone();
    cv::Mat arry(1, m * n, CV_8U);    // 局部矩阵

    cv::copyMakeBorder(input, input, (m - 1) / 2, (m - 1) / 2, (n - 1) / 2, (n - 1) / 2, cv::BORDER_REFLECT);

    cv::Mat mean1, stddev1, mean2, stddev2;
    cv::meanStdDev(input, mean1, stddev1);    // 获取矩阵平均值和标准差
    double _stddev1, _mean2, _stddev2;        // 图像标准差、局部均值和局部标准差
    _stddev1 = stddev1.at<double>(0, 0);

    for (int i = (m - 1) / 2; i < input.rows - (m - 1) / 2; i ++)
        for (int j = (n - 1) / 2; j < input.cols - (n - 1) / 2; j ++)
        {
            int h = 0;
            for (int x = -(m - 1) / 2; x <= (m - 1) / 2; x ++)
                for (int y = -(n - 1) / 2; y <= (n - 1) / 2; y ++)
                {
                    arry.at<uchar>(h) = input.at<uchar>(i + x, j + y);
                    h ++;
                }

            cv::meanStdDev(arry, mean2, stddev2);
            _stddev2 = stddev2.at<double>(0, 0);
            _mean2 = mean2.at<double>(0, 0);

            double k = (_stddev1 * _stddev1) / (_stddev2 * _stddev2 + 0.00001);
            if (k <= 1)
                output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = input.at<uchar>(i, j) - k * (input.at<uchar>(i, j) - _mean2);
            else
                output.at<uchar>(i - (m - 1) / 2, j - (n - 1) / 2) = _mean2;
        }

}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output;

    GaussianNoise(input, input);    //添加高斯噪声

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", input);

    AdaptiveLocalNoiseReductionFilter(input, output, 7, 7);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", output);


    cv::waitKey(0);
    return 0;
}

效果展示：

自适应局部均值滤波器

自适应中值滤波器

通过判断，将中值或者原像素灰度值作为结果。记以下符号：

zminz_{min} 是 SxyS_{xy} 中的最小灰度值；zmaxz_{max} 是 SxyS_{xy} 中的最大灰度值；zmedz_{med} 是 SxyS_{xy} 中灰度值的中值；

zxyz_{xy} 是坐标 (x,y)(x,y) 处的灰度值， SmaxS_{max} 是 SxyS_{xy} 允许的最大尺寸。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <iostream>
#include <vector>
#include <opencv2/opencv.hpp>
#include "Salt.h"

// 添加高斯噪声
void GaussianNoise(cv::Mat input, cv::Mat &output)
{
    cv::RNG rng;
    cv::Mat noice = input.clone();
    output = input.clone();
    rng.fill(noice, cv::RNG::NORMAL, 10, 50);    // 使用NORMAL参数添加高斯噪声
    output = input + noice;
}

// 求输出值
uchar AdaptiveMedian(cv::Mat input, int i, int j, int filter_size, int maxsize)
{
    int num = filter_size * filter_size;
    std::vector<uchar> arry(num);
    int h = 0;
    for (int x = -(filter_size - 1) / 2; x <= (filter_size - 1) / 2; x ++)
        for (int y = -(filter_size - 1) / 2; y <= (filter_size - 1) / 2; y ++)
        {
            arry[h] = input.at<uchar>(i + x, j + y);
            h ++;
        }
    sort(arry.begin(), arry.end());
    int z_min = arry[0];
    int z_med = arry[(num - 1) / 2];
    int z_max = arry[num - 1];
    int z_xy = input.at<uchar>(i, j);

    if (z_med > z_min and z_med < z_max)
    {
        if (z_xy > z_min and z_xy < z_max)
            return z_xy;
        else return z_med;
    }

    else
    {
        filter_size += 2;
        if (filter_size <= maxsize)
            return AdaptiveMedian(input, i, j, filter_size, maxsize);
        else return z_med;
    }
}

// 自适应中值滤波器
void AdaptiveMedianFilter(cv::Mat input, cv::Mat &output, int maxsize)
{
    output = input.clone();

    cv::copyMakeBorder(input, input, (maxsize - 1) / 2, (maxsize - 1) / 2, (maxsize - 1) / 2, (maxsize - 1) / 2, cv::BORDER_REFLECT);

    for (int i = (maxsize - 1) / 2; i < input.rows - (maxsize - 1) / 2; i ++)
        for (int j = (maxsize - 1) / 2; j < input.cols - (maxsize - 1) / 2; j ++)
        {
            int filter_size = 3;    // 开始时滤波器尺寸
            output.at<uchar>(i - (maxsize - 1) / 2, j - (maxsize - 1) / 2) = AdaptiveMedian(input, i, j, filter_size, maxsize);
        }
}

int main()
{
    cv::Mat input = cv::imread("src/test.jpg", 0);
    cv::Mat output1, output2;

    cv::Mat noise1 = input.clone(), noise2 = input.clone();

    GaussianNoise(input, noise1);    // 添加高斯噪声
    Salt(input, noise2, 100000);            // 添加盐粒噪声

    cv::namedWindow("高斯噪声", cv::WINDOW_NORMAL);
    cv::imshow("高斯噪声", noise1);
    cv::namedWindow("盐粒噪声", cv::WINDOW_NORMAL);
    cv::imshow("盐粒噪声", noise2);

    AdaptiveMedianFilter(noise1, output1, 7);
    AdaptiveMedianFilter(noise2, output2, 7);

    cv::namedWindow("降低高斯噪声", cv::WINDOW_NORMAL);
    cv::imshow("降低高斯噪声", output1);
    cv::namedWindow("降低盐粒噪声", cv::WINDOW_NORMAL);
    cv::imshow("降低盐粒噪声", output2);


    cv::waitKey(0);
    return 0;
}
1
2
3
4
5
6
// Salt.h
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, cv::Mat &output, int n);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// Salt.cpp
#include "Salt.h"

void Salt(cv::Mat input, cv::Mat &output, int n)
{
    output = input.clone();
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            output.at<uchar>(i, j) = 255;
        else if (input.channels() == 3)
            output.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255);
    }
}

效果展示；

对于盐粒噪声有奇效

自适应中值滤波器

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。