傅里叶变换

傅里叶级数

傅里叶级数：任何周期函数都可表示为不同频率的正弦函数和或余弦函数和，其中每个正弦函数和或余弦函数和都有不同的系数。

f(t)=∑n=−∞∞cnej2πnTtf(t)=\sum_{n=-\infty}^\infty c_ne^{j\frac {2\pi n} {T}t}

其中，

cn=1T∫−T/2T/2f(t)e−j2πnTtdt,n=0,±1,±2,…c_n=\frac 1T\int_{-T/2}^{T/2}f(t)e^{-j\frac {2\pi n} {T}t}dt,n=0,\pm 1,\pm 2,…

是系数。此篇j表示虚数单位： j2=−1j^2=-1 。

傅里叶变换

傅里叶变换：（曲线下方面积有限的）非周期函数也能用正弦函数和/或余弦函数乘以加权函数的积分来表示

这表明用傅里叶级数或变换表示的函数可由逆过程完全重建（复原），而不丢失信息；允许我们工作在傅里叶域，然后返回到函数的原始域中，而不会丢失任何信息。

计算机慢慢出现了快速傅里叶变换算法（FFT），使用FFT进行频率域处理比不可分离核的空间域处理要快。

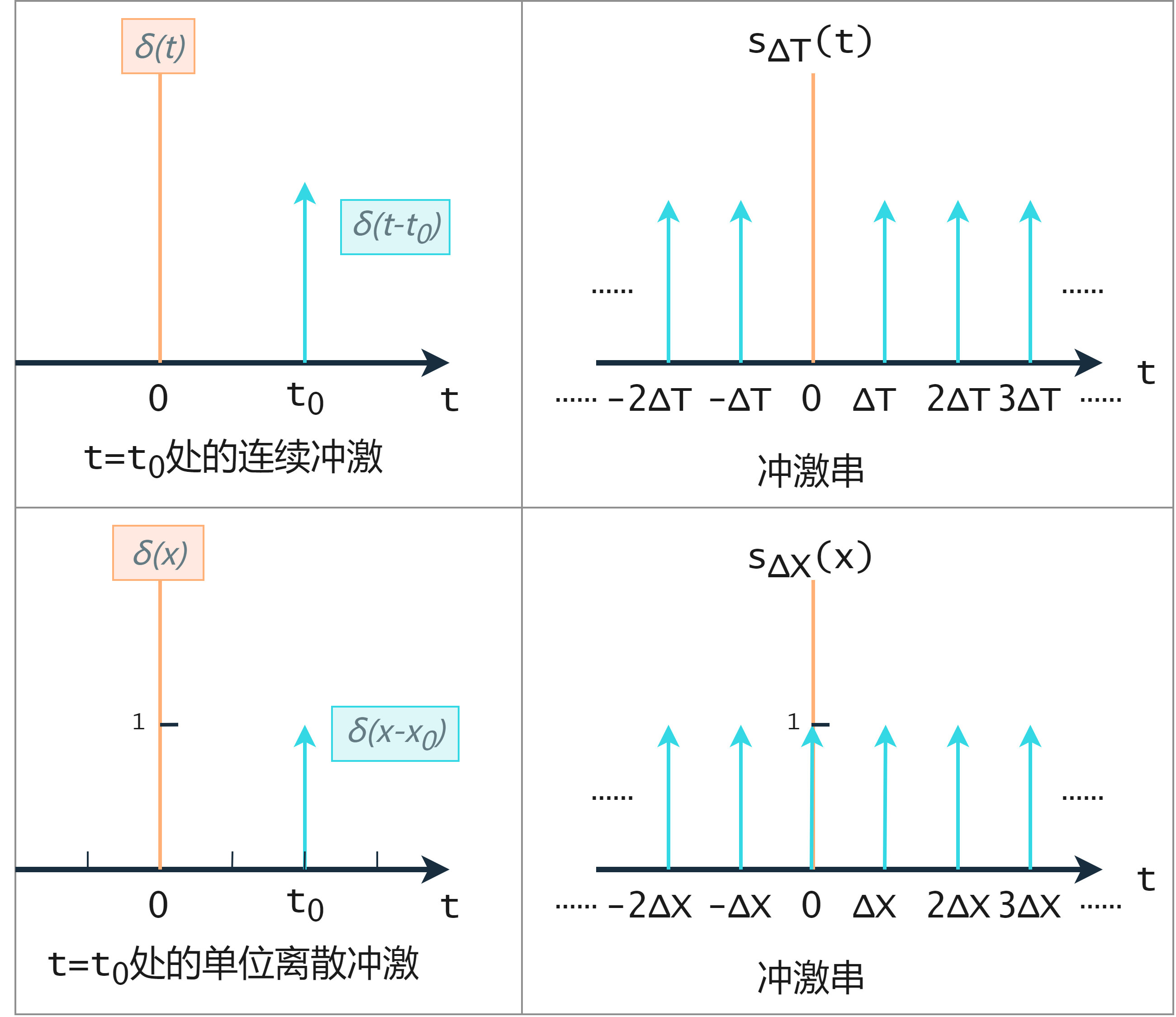
冲激函数及其取样（筛选）性质

连续变量t在t=0处的单位冲激表示为 δ(t)\delta(t) ，其定义为：

δ(t)={∞,t=00,t≠0\delta(t)=\begin{cases} \infty,&t=0\\ 0, &t\neq 0 \end{cases}

该定义被限制满足：

∫−∞∞δ(t)dt=1\int_{-\infty}^{\infty}\delta(t)dt=1

当t解释为时间时，冲激可视作幅度为无线、持续时间为0、具有单位面积的尖峰信号。

冲激具有关于积分的所谓 取样性质 ：

∫−∞∞f(t)δ(t)dt=f(0)\int_{-\infty}^{\infty}f(t)\delta(t)dt=f(0)

对其一般化，任意一点 t0t_0 的冲激表示为 δ(t−t0)\delta(t-t_0) ，有：

∫−∞∞f(t)δ(t−t0)dt=f(t0)\int_{-\infty}^{\infty}f(t)\delta(t-t_0)dt=f(t_0)

举一个小例子，取 f(t)=cos⁡(t)f(t)=\cos(t) ，则使用冲激 δ(t−π)\delta(t-\pi) 得到取样 f(π)=cos⁡(π)=−1f(\pi)=\cos(\pi)=-1 。

冲激串则是无穷多个冲激 ΔT\Delta T 单位的和：

sΔT(t)=∑k=−∞∞δ(t−kΔT)s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}\delta(t-k\Delta T)

单位离散冲激 δ(x)\delta(x) 在离散系统的作用域处理连续变量时冲激 δ(t)\delta(t) 作用相同，定义为：

δ(x)={1,x=00,x≠0\delta(x)=\begin{cases} 1,&x=0\\ 0, &x\neq 0 \end{cases}

该定义被限制的离散等效形式为：

∑x=−∞∞δ(x)=1\sum_{x=-\infty}^{\infty}\delta(x) = 1

离散变量的取样性质的形式为：

∑x=−∞∞f(x)δ(x)=f(0)\sum_{x=-\infty}^{\infty}f(x)\delta(x)=f(0)

一般式为：

∑x=−∞∞f(x)δ(x−x0)=f(x0)\sum_{x=-\infty}^{\infty}f(x)\delta(x-x_0)=f(x_0)

小结：

项 连续变量t 离散变量x
在0处的单位冲激 δ(t)={∞,t=00,t≠0\delta(t)=\begin{cases}\infty,&t=0\\0, &t\neq 0\end{cases} δ(x)={1,x=00,x≠0\delta(x)=\begin{cases}1,&x=0\\0, &x\neq 0\end{cases}
单位冲激满足 ∫−∞∞δ(t)dt=1\int_{-\infty}^{\infty}\delta(t)dt=1 ∑x=−∞∞δ(x)=1\sum_{x=-\infty}^{\infty}\delta(x) = 1
取样性质 ∫−∞∞f(t)δ(t)dt=f(0)\int_{-\infty}^{\infty}f(t)\delta(t)dt=f(0) ∑x=−∞∞f(x)δ(x)=f(0)\sum_{x=-\infty}^{\infty}f(x)\delta(x)=f(0)
取样性质一般化 ∫−∞∞f(t)δ(t−t0)dt=f(t0)\int_{-\infty}^{\infty}f(t)\delta(t-t_0)dt=f(t_0) ∑x=−∞∞f(x)δ(x−x0)=f(x0)\sum_{x=-\infty}^{\infty}f(x)\delta(x-x_0)=f(x_0)

冲激串：

sΔT(t)=∑k=−∞∞δ(t−kΔT)s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}\delta(t-k\Delta T)

连续单变量函数的傅里叶变换

连续变量t的连续函数f(t)的傅里叶变换 ℑ{f(t)}\Im\{f(t)\} 表示，它定义为：

ℑ{f(t)}=∫−∞∞f(t)e−j2πμtdt\Im\{f(t)\}=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt

上式中， μ\mu 为连续变量，积分变量为t，所以 ℑ{f(t)}\Im\{f(t)\} 只是 μ\mu 的函数，即 ℑ{f(t)}=F(μ)\Im\{f(t)\}=F(\mu) ，所以 f(t)f(t) 的傅里叶变换也可以写为：

F(μ)=∫−∞∞f(t)e−j2πμtdt①F(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt \quad ①

相反，已知 F(μ)F(\mu) 是可以通过傅里叶反变换得到 f(t)f(t) ，为：

f(t)=∫−∞∞F(μ)ej2πμtdt②f(t)=\int_{-\infty}^{\infty}F(\mu)e^{j2\pi \mu t}dt\quad ②

称①式和②式共同构成傅里叶变换对，通常表示为 f(t)⇔F(μ)f(t) \Leftrightarrow F(\mu) 。双箭头表明傅里叶正变换得到右侧表达式，而左侧表达式是取右侧表达式的傅里叶反变换得到。

利用欧拉公式 ejθ=cos⁡θ+jsin⁡θe^{j\theta}=\cos\theta+j\sin\theta ，将式①变成

F(μ)=∫−∞∞f(t)[cos⁡(2πμt)−jsin⁡(2πμt)]dtF(\mu)=\int_{-\infty}^{\infty}f(t)[\cos(2\pi\mu t)-j\sin(2\pi\mu t)]dt

可以看到，如果f(t)为实数，则变换通常是复数。傅里叶变换式f(t)乘以正弦函数的展开式，而其中正弦函数的频率由 μ\mu 值决定。因此积分后留下的唯一变量是频率，故称傅里叶变换域是频率域。

讨论中， tt 可以表示任何连续变量，并且频率变量 μ\mu 的单位取决于 tt 的单位。

举个例子：

简单连续函数的傅里叶变换

对盒式函数进行傅里叶变换，有

F(μ)=∫−∞∞f(t)e−j2πμtdt=∫−W/2W/2Ae−j2πμtdt=−Aj2πμ[e−j2πμt]−W/2W/2=−Aj2πμ[e−jπμW−ejπμW]=Aj2πμ[ejπμW−e−jπμW]=AWsin⁡(πμW)πμWF(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi\mu t}dt=\int_{-W/2}^{W/2}Ae^{-j2\pi\mu t}dt\\ =\frac {-A} {j2\pi\mu}\Big[e^{-j2\pi\mu t}\Big]^{W/2}_{-W/2}=\frac {-A} {j2\pi\mu}\Big[e^{-j\pi\mu W}-e^{j\pi\mu W}\Big]\\ =\frac {A} {j2\pi\mu}\Big[e^{j\pi\mu W}-e^{-j\pi\mu W}\Big]=AW\frac {\sin(\pi\mu W)} {\pi\mu W}

上式用到了 sin⁡θ=(ejθ−e−jθ)/2j\sin\theta=(e^{j\theta}-e^{-j\theta})/2j

傅里叶变换中包含复数项，这是为了显示变换的幅值（一个实量）的一种约定。这个幅值称为傅里叶频谱或频谱：

∣F(μ)∣=AW∣sin⁡(πμW)πμW∣\vert F(\mu)\vert=AW\vert\frac{\sin(\pi\mu W)} {\pi\mu W}\vert

F(μ)F(\mu) 与频率的关系曲线如下：

该曲线的关键性质：

  1. F(μ)F(\mu) 和 ∣F(μ)∣\vert F(\mu)\vert 的零值都与盒式函数的宽度W成反比；

  2. 到原点的距离越大，旁瓣的高度随到原点的举例增加而减小；

  3. 函数向μ的正负方向无限扩展。

再举一个冲激傅里叶变换的例子。

位于原点的单位冲激的傅里叶变换由上面式①得：

ℑ{δ(t)}=F(μ)=∫−∞∞f(t)e−j2πμtdt=∫∞∞δ(t)e−j2πμtdt=e−j2πμ0=e0=1\Im \{\delta(t)\}=F(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt=\int_{\infty}^{\infty}\delta(t)e^{-j2\pi\mu t}dt=e^{-j2\pi\mu_0}=e^0=1

这就是空间域原点位置的一个冲激的傅里叶变换，在频率域中是一个常数。

当 t=t0t=t_0 处一个冲击傅里叶变换是：

ℑ{δ(t)}=F(μ)=∫∞∞δ(t−t0)e−j2πμtdt=∫−∞∞e−j2πμtδ(t−t0)dt=e−j2πμt0\Im \{\delta(t)\}=F(\mu)=\int_{\infty}^{\infty}\delta(t-t_0)e^{-j2\pi\mu t}dt=\int_{-\infty}^{\infty}e^{-j2\pi\mu t}\delta(t-t_0)dt=e^{-j2\pi\mu t_0}

上式使用了取样一般化性质。 e−j2πμt0e^{-j2\pi\mu t_0} 表示中心在复平面原点的一个单位圆。

观察式①式②

F(μ)=∫−∞∞f(t)e−j2πμtdtf(t)=∫−∞∞F(μ)ej2πμtdtF(\mu)=\int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt \\ f(t)=\int_{-\infty}^{\infty}F(\mu)e^{j2\pi \mu t}dt\quad

发现只有指数符号不同。因此如果函数f(t)有傅里叶变换F(μ)，那么求该函数在点t的值F(t)时，一定有变换f(-μ)。利用这种对称性质，将冲激 δ(t−t0)\delta(t-t_0) 的傅里叶变换 e−j2πμt0e^{-j2\pi\mu t_0} 得到函数 e−j2πμt0e^{-j2\pi\mu t_0} 的变换为 δ(−μ−t0)\delta(-\mu-t_0) 。令 −t0=a-t_0=a ，可得 ej2πate^{j2\pi a t} 的变换是 δ(−μ+a)=δ(μ+a)\delta(-\mu+a)=\delta(\mu+a)

冲激串 sΔT(t)s_{\Delta T}(t) 是周期为 ΔT\Delta T 的周期函数：

sΔT(t)=∑k=−∞∞δ(t−kΔT)s_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}\delta(t-k\Delta T)

因此可以表示为傅里叶级数：

sΔT(t)=∑k=−∞∞cnej2πnΔTt,cn=1ΔT∫−ΔT/2ΔT/2SΔT(t)e−j2πnΔTtdts_{\Delta T}(t)=\sum_{k=-\infty}^{\infty}c_ne^{j\frac{2\pi n} {\Delta T}t},\\ c_n=\frac{1} {\Delta T}\int_{-\Delta T/2}^{\Delta T/2}S_{\Delta T}(t)e^{-j\frac{2\pi n} {\Delta T}t}dt

由于区间 [−ΔT/2,ΔT/2]\big[-\Delta T/2,\Delta T/2\big] 上积分仅包含原点的冲激，故上式简化为：

cn=1ΔT∫−ΔT/2ΔT/2δ(t)e−j2πnΔTtdt=1ΔTe0=1ΔTc_n=\frac{1} {\Delta T}\int_{-\Delta T/2}^{\Delta T/2}\delta(t)e^{-j\frac{2\pi n} {\Delta T}t}dt=\frac{1} {\Delta T}e^0=\frac{1} {\Delta T}

于是傅里叶级数变成：

sΔT(t)=1ΔT∑n=−∞∞ej2πnΔTts_{\Delta T}(t)=\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}e^{j\frac{2\pi n} {\Delta T}t}

由 ℑ{δ(t−t0)}=e−j2πμt0\Im \{\delta(t-t_0)\}=e^{-j2\pi\mu t_0} ，得到：

ℑ{ej2πnΔTt}=δ(μ−nΔT)\Im \{e^{j\frac{2\pi n} {\Delta T}t}\}=\delta(\mu-\frac{n} {\Delta T})

再由于和的傅里叶变换等于各分量的傅里叶变换之和，所以周期冲激串的傅里叶变换 S(μ)S(\mu) 是：

S~(μ)=ℑ{sΔT(t)}=ℑ{1ΔT∑n=−∞∞ej2πnΔTt}=1ΔTℑ{∑n=−∞∞ej2πnΔTt}=1ΔT∑n=−∞∞δ(μ−nΔT)\tilde{S}(\mu)=\Im\{s_{\Delta T}(t)\}=\Im\{\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}e^{j\frac{2\pi n} {\Delta T}t}\}=\frac{1} {\Delta T}\Im\{\sum_{n=-\infty}^{\infty}e^{j\frac{2\pi n} {\Delta T}t}\}=\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}\delta(\mu-\frac{n} {\Delta T})

上述结果可得，周期为 ΔT\Delta T 的冲激串的傅里叶变换仍然是冲激串，其周期变为 1/ΔT1/\Delta T。

傅里叶变换与卷积

卷积：空间域中两个函数的卷积的傅里叶变换，等于频率域中两个函数的傅里叶变换的乘积。

设f(t)和h(t)为两个连续函数，F(t)和H(t)为f(t)和h(t)的傅里叶变换，则有：

(f★h)(t)⇔(H⋅F)(μ)(f⋅h)(t)⇔(H★F)(μ)(f★h)(t)\Leftrightarrow(H\cdot F)(\mu)\\ (f\cdot h)(t)\Leftrightarrow(H★F)(\mu)

取样和取样函数的傅里叶变换

取样：对连续函数转换为一系列的离散值。

f~(t)=f(t)sΔT(t)=∑n=−∞∞f(t)δ(t−nΔT)\tilde{f}(t)=f(t)s_{\Delta T}(t)=\sum_{n=-\infty}^{\infty}f(t)\delta(t-n\Delta T)

fk=∫−∞∞f(t)δ(t−kΔT)dt=f(kΔT)f_k=\int_{-\infty}^{\infty}f(t)\delta(t-k\Delta T)dt=f(k\Delta T)

对取样后的函数 f~(t)\tilde{f}(t) 的傅里叶变换 F~(μ)\tilde{F}(\mu) 是：

F~(μ)=ℑ{f~(t)}=ℑ{f(t)sΔT(t)}=(F★S)(μ)\tilde{F}(\mu)=\Im\{\tilde{f}(t)\}=\Im\{f(t)s_{\Delta T}(t)\}=(F★S)(\mu)

其中， S(μ)S(\mu) 是冲激串的傅里叶变换：

S(μ)=1ΔT∑n=−∞∞δ(μ−nΔT)S(\mu)=\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}\delta(\mu-\frac{n} {\Delta T})

直接得 F(μ)F(\mu) 和 S(μ)S(\mu) 的卷积：

F~(μ)=(F★S)(μ)=∫−∞∞F(τ)S(μ−τ)dτ=1ΔT∫−∞∞F(τ)∑n=−∞∞δ(μ−τ−nΔT)dτ=1ΔT∑n=−∞∞∫−∞∞F(τ)δ(μ−τ−nΔT)dτ=1ΔT∑n=−∞∞F(μ−nΔT)\tilde{F}(\mu)=(F★S)(\mu)=\int_{-\infty}^{\infty}F(\tau)S(\mu-\tau)d\tau\\ =\frac{1} {\Delta T}\int_{-\infty}^{\infty}F(\tau)\sum_{n=-\infty}^{\infty}\delta\big(\mu-\tau-\frac{n} {\Delta T}\big)d\tau\\ =\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}F(\tau)\delta\big(\mu-\tau-\frac{n} {\Delta T}\big)d\tau\\ =\frac{1} {\Delta T}\sum_{n=-\infty}^{\infty}F(\mu-\frac{n} {\Delta T})

单变量离散傅里叶变换DFT

一维离散傅里叶变换：

Fm=∑n=0M−1fne−j2πmn/M,m=0,1,2…,M−1F_m=\sum_{n=0}^{M-1}f_ne^{-j2\pi mn/M},m=0,1,2…,M-1

一维离散傅里叶逆变换：

fn=1M∑m=0M−1Fmej2πmn/M,n=0,1,2…,M−1f_n=\frac{1} {M}\sum_{m=0}^{M-1}F_me^{j2\pi mn/M},n=0,1,2…,M-1

二变量离散傅里叶变换

二维离散傅里叶变换：

F(μ,ν)=∑x=0M−1∑y=0N−1f(x,y)e−j2π(μx/M+νy/N)F(\mu,\nu)=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\mu x/M+\nu y/N)}

二维离散傅里叶逆变换：

f(x,y)=1MN∑x=0M−1∑y=0N−1F(μ,ν)ej2π(μx/M+νy/N)f(x,y)=\frac{1} {MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}F(\mu,\nu)e^{j2\pi(\mu x/M+\nu y/N)}

参考代码

先了解以下函数：

1
int getOptimalDFTSize(int vecsize)

vecsize为向量尺寸大小，该函数用于返回给定向量尺寸经过DFT变换后结果的最优尺寸大小。

1
void copyMakeBorder(InputArray src, OutputArray dst, int top, int bottom, int left, int right, int borderType, const Scalar& value = Scalar())

该函数用于扩充图像边界，参数如下：

  • src：输入图像；

  • dst：输出与输入图像相同类型图像；

  • top、bottom、left、right：在图像的四个方向上扩充像素值；

  • borderType：边界类型，常见取值为BORDER_CONSTANT；

  • value：边界类型为BORDER_CONSTANT时表示边界值。

1
void dft(InputArray src, OutputArray dst, int flags = 0, int nonzeroRows = 0)

该函数为OpenCV提供的傅里叶变换函数，参数如下：

  • src：输入图像；

  • dst：输出图像；

  • flags：转换标识符，默认为0。也有以下取值，DFT_INVERSE（用一维或二维逆变换取代默认的正向变换）、DFT_SCALE（缩放比例标识符，根据数据元素个数平均求出缩放结果）、DFT_ROWS（对输入矩阵的每行进行正向或反向傅里叶变换）、DFT_COMPLEX_OUTPUT（对一维或二维实数数组进行正向变换，结果是复数阵列，是默认）、DFT_REAL_OUTPUT（对一维或二维复数数组进行逆向变换）；

  • nonzeroRows：当其不为0时函数会假设输入数组（没有设置DFT_INVERSE）的第一行或第一个输出数组（设置了DFT_INVERSE）包含非零值。

1
void magnitude(InputArray x, InputArray y, OutputArray magnitude)

该函数用于计算二维矢量的幅值，参数如下：

  • x：浮点型数组的x坐标矢量，即实部；

  • y：浮点型数组的y坐标矢量，必须和x尺寸相同；

  • magnitude：与x类型和尺寸相同的输出数组；

其计算公式为：

dst(I)=x(I)2+y(I)2dst(I)=\sqrt{x(I)^2+y(I)^2} 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <opencv2/opencv.hpp>
#include <iostream>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_img)
{
    // 拓展图像矩阵，为2，3，5的倍数时运算速度快
    int m = cv::getOptimalDFTSize(input.rows);
    int n = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, m - input.rows, 0, n - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 创建planes存储复数的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(),CV_32F) };

    // 从多个单通道数组中创建一个多通道数组trf_img。
    // 函数Merge将几个数组合并为一个多通道阵列，即输出数组的每个元素将是输入数组元素的级联
    cv::merge(planes, 2, trf_img);  

    // 进行傅里叶变换
    cv::dft(trf_img, trf_img);

    // 将trf_img拆分到planes数组
    cv::split(trf_img, planes);

    // 计算复数的幅值，即频谱图，保存在output
    cv::magnitude(planes[0], planes[1], output);

    // 赋值计算过大，进行处理
    output += cv::Scalar(1);    //像素加一防止log(0)
    log(output, output);    // 进行对数运算
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);   // 归一化

    // 剪切和重分布幅度图像限
    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    // 重新排列傅里叶图像中的象限，使原点位于图像中心
    int cx = output.cols / 2;
    int cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy));
    cv::Mat q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy));
    cv::Mat q3(output, cv::Rect(cx, cy, cx, cy));

    // 交换象限中心化
    cv::Mat tmp;
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

}

int main()
{
    cv::Mat image = cv::imread("src/test.jpg", 0);
    cv::Mat image_output, image_trf;

    cv::namedWindow("灰度图", cv::WINDOW_NORMAL);
    cv::imshow("灰度图", image);

    DFT(image, image_output, image_trf);

    cv::namedWindow("频谱图", cv::WINDOW_NORMAL);
    cv::imshow("频谱图", image_output);

    cv::waitKey(0);
    return 0;
}

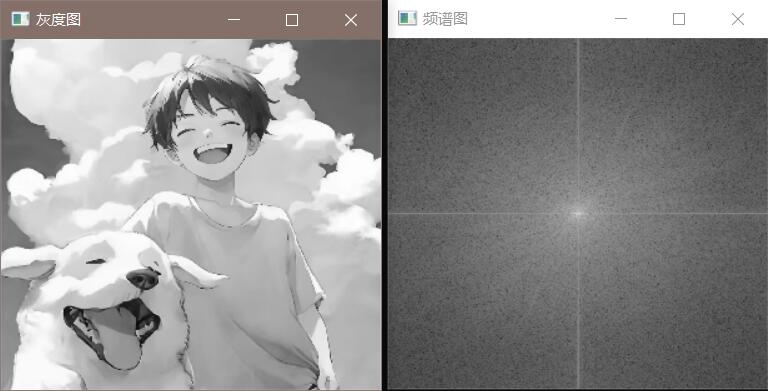
效果展示：

频谱图

频谱图有以下规律：

  1. 频谱图从中心点到四周，频率越来越大；

  2. 频谱图中心点一般最亮，与原图像平均亮度相关；

  3. 频率域滤波就是改变频谱图中高频率或者低频率的值.

  4. 频谱图中的点关于中心点对称，对称的两点表示某个频率的波。

  5. 两个对称点离中心点的距离代表频率的高低，离中心点越远代表的频率越高。

  6. 两个对称点的亮度表示波的幅值，越亮幅值越大。

  7. 图像中，低频率代表灰度变化缓慢的信息；高频率代表变化剧烈的信息，如边缘及噪声等。在6中，低频区越亮代表变化缓慢的区域较多，高频区越亮代表图像细节很多。

  8. 对称点所在直线的方向为波的方向，与原图中对应的线性信息垂直。如下图，图中有一组平行的线，在频谱图垂直方向也有一条较亮的线（可用于方向滤波，增强或者滤除某个方向的线性特征）。

低通滤波

理想低通滤波

通过设置频率半径，半径内的频率大小不变，半径外的频率置为0，保留了低频区，滤除了高频区。

传递函数为：

H(u,v)={1,D(u,v)≤D00,D(u,v)>D0H(u,v)= \begin{cases} 1,\quad D(u,v)\leq D_0\\ 0, \quad D(u,v)>D_0 \end{cases}

其中， D0D_0 是一个正常数， D(u,v)D(u,v) 是频率域中点(u,v)到P×Q频率矩形中心的距离， D(u,v)=[(u−P/2)2+(v−Q/2)2]1/2D(u,v)=[(u-P/2)^2+(v-Q/2)^2]^{1/2} 。

理想低通滤波器由于进行傅里叶变换和傅里叶逆变换时的差异，会导致振铃效应，一般很少使用。

振铃效应：指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"
#include "Salt.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    Salt(image, 100000);    // 添加100k个噪点

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 理想低通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
            if ((i - cx) * (i - cx) + (j - cy) * (j - cy) > r * r)
            {
                trf_real.at<float>(i, j) = 0;
                trf_imag.at<float>(i, j) = 0;
            }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

为了更好的效果，手动添加噪声：

1
2
3
4
5
6
// Salt.h
#pragma once
#include <opencv2/opencv.hpp>
#include <random>

void Salt(cv::Mat input, int n);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 噪声文件Salt.cpp
#include "Salt.h"

void Salt(cv::Mat input, int n)
{
    std::default_random_engine generator;
    std::uniform_int_distribution<int>row(0, input.rows - 1);
    std::uniform_int_distribution<int>col(0, input.cols - 1);
    int i, j;
    for (int k = 0; k < n; k ++)
    {
        i = row(generator);
        j = col(generator);
        if (input.channels() == 1)
            input.at<uchar>(i, j) = 255;
        else if (input.channels() == 3)
            input.at<cv::Vec3b>(i, j) = cv::Vec3b(255, 255, 255);
    }
}

对图像傅里叶变换：

1
2
3
4
5
6
// DFT.h
#pragma once
#include <opencv2/opencv.hpp>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// DFT.cpp
#include "DFT.h"

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr)
{
    // 扩展图像，优化速度
    int n = cv::getOptimalDFTSize(input.rows);
    int m = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, n - input.rows, 0, m - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 用于存储傅里叶变换的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(), CV_32F) };

    cv::merge(planes, 2, trf_arr);

    cv::dft(trf_arr, trf_arr);

    cv::split(trf_arr, planes);
    cv::Mat trf_img_real = planes[0];
    cv::Mat trf_img_imag = planes[1];

    // 计算复数的幅值，保存在output中
    cv::magnitude(planes[0], planes[1], output);

    // 优化幅值大小
    output += cv::Scalar(1);
    log(output, output);
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);

    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    int cx = output.cols / 2, cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy)), q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy)), q3(output, cv::Rect(cx, cy, cx, cy));
    cv::Mat tmp;

    // 交换区域使得原点位于中心
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

    // 复数的实数部分交换
    cv::Mat q00(trf_img_real, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q01(trf_img_real, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q02(trf_img_real, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q03(trf_img_real, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q00.copyTo(tmp); q03.copyTo(q00); tmp.copyTo(q03);        //左上与右下进行交换
    q01.copyTo(tmp); q02.copyTo(q01); tmp.copyTo(q02);        //右上与左下进行交换

    // 复数的虚数部分交换
    cv::Mat q10(trf_img_imag, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q11(trf_img_imag, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q12(trf_img_imag, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q13(trf_img_imag, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q10.copyTo(tmp); q13.copyTo(q10); tmp.copyTo(q13);        //左上与右下进行交换
    q11.copyTo(tmp); q12.copyTo(q11); tmp.copyTo(q12);        //右上与左下进行交换

    planes[0] = trf_img_real;
    planes[1] = trf_img_imag;
    cv::merge(planes, 2, trf_arr);    // 将傅里叶变换的复数结果保存在trf_arr
}

效果展示：

r=120

高斯低通滤波

高斯低通滤波器的传递函数为：

H(u,v)=e−D2(u,v)/2σ2H(u,v)=e^{-D^2(u,v)/2\sigma^2}

其中， D(u,v)D(u,v) 是P×Q频率矩形中心到矩形中包含的任意一点(u,v)的距离，令 σ=D0\sigma=D_0 ，

H(u,v)=e−D2(u,v)/2D02H(u,v)=e^{-D^2(u,v)/2D_0^2}

那么 D0D_0 是截止频率（设置半径）。当 D(u,v)=D0D(u,v)=D_0 时，高斯低通滤波器传递函数下降到其最大值1.0的0.607。

由于高斯函数的傅里叶变换还是高斯函数，所以高斯低通滤波器没有振铃效应。

代码：

DFT.h、DFT.cpp、Salt.h、Salt.cpp同上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"
#include "Salt.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    Salt(image, 100000);    // 添加100k个噪点

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 高斯低通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 80;    // 滤波半径
    float h;

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            h = exp(-((i - cx) * (i - cx) + (j - cy) * (j - cy)) / (2.0 * r * r));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

r=80

巴特沃斯低通滤波

巴特沃斯低通滤波器的传递函数为：

H(u,v)=11+[D(u,v)/D0]2nH(u,v)=\frac {1} {1+[D(u,v)/D_0]^{2n} }

其中， D(u,v)D(u,v) 是P×Q频率矩形中心到矩形中包含的任意一点(u,v)的距离， D0D_0 是截止频率（设置半径）， nn 是巴特沃斯滤波器的阶数。

1阶巴特沃斯滤波器既没有振铃效应也没有负值；2阶巴特沃斯滤波器有轻微振铃效应和较小的负值，但比理想低通滤波器好；高阶巴特沃斯滤波器具有非常明显的振铃效应。2阶和3阶的巴特沃斯滤波器较为合适。

代码：

DFT.h、DFT.cpp、Salt.h、Salt.cpp同上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"
#include "Salt.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    Salt(image, 100000);    // 添加100k个噪点

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 巴特沃斯低通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径
    float h;
    float n = 3;    // 巴特沃斯滤波器阶数
    float d;        // 任意点到中心的距离

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = 1.0 / (1 + pow((d / (r * r)), 2 * n));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

r=120,n=3

高通滤波

理想高通滤波

通过设置频率半径，半径外的频率大小不变，半径内的频率置为0，保留了高频区，滤除了低频区。

而边缘和其他灰度的急剧变化与高频分量有关，故高通滤波器可以实现边缘锐化。

传递函数为：

H(u,v)={0,D(u,v)≤D01,D(u,v)>D0H(u,v)= \begin{cases} 0,\quad D(u,v)\leq D_0\\ 1, \quad D(u,v)>D_0 \end{cases}

其中， D0D_0 是一个正常数， D(u,v)D(u,v) 是频率域中点(u,v)到P×Q频率矩形中心的距离， D(u,v)=[(u−P/2)2+(v−Q/2)2]1/2D(u,v)=[(u-P/2)^2+(v-Q/2)^2]^{1/2} 。

代码（DFT代码文件见最后）：

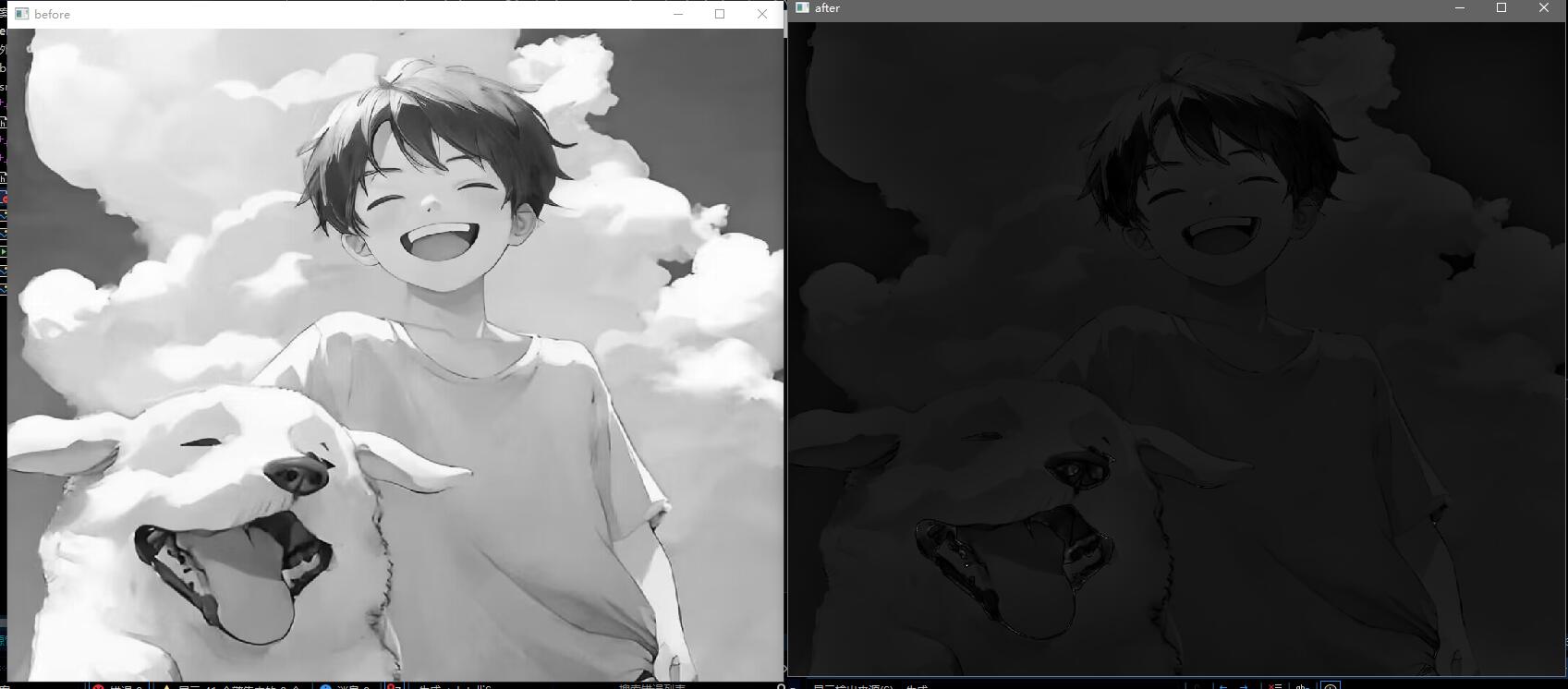
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 理想高通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
            if ((i - cx) * (i - cx) + (j - cy) * (j - cy) < r * r)
            {
                trf_real.at<float>(i, j) = 0;
                trf_imag.at<float>(i, j) = 0;
            }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

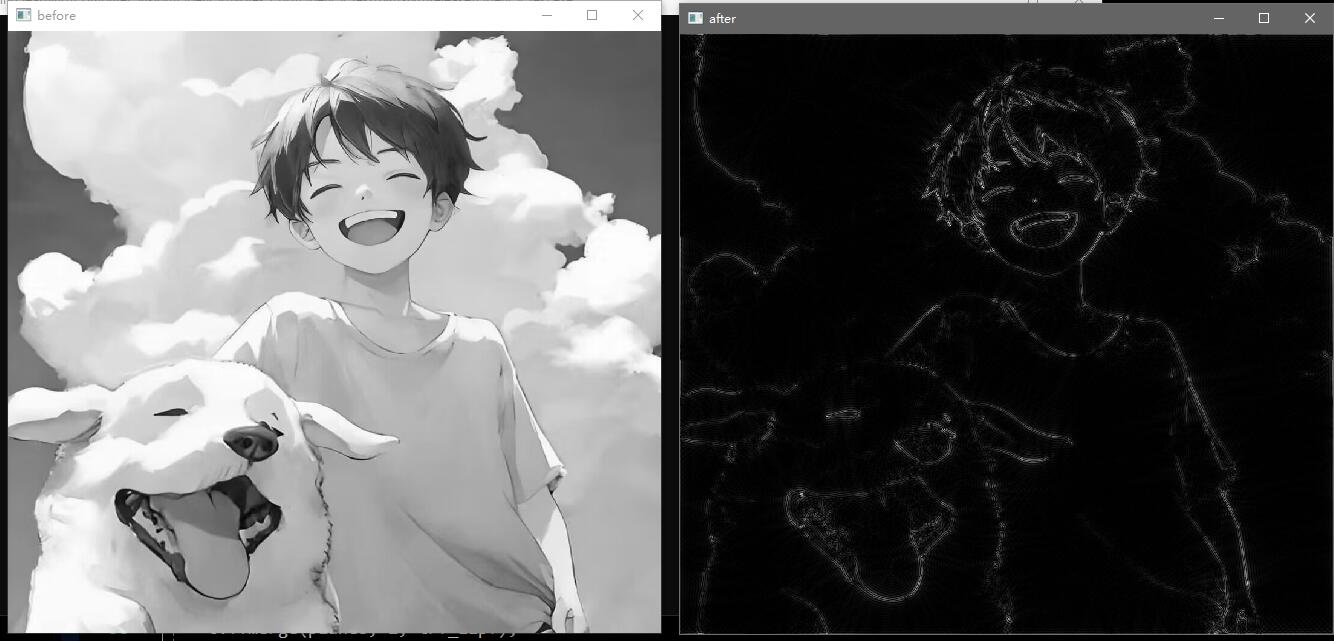
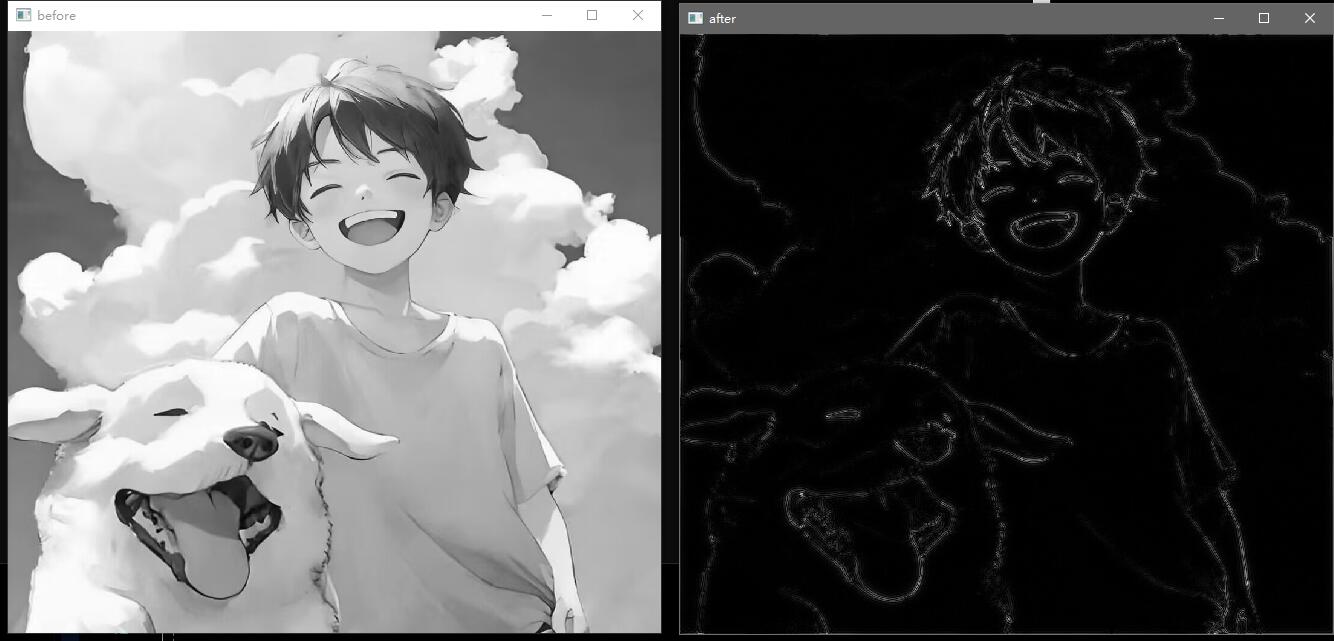
效果展示：

r=120

高斯高通滤波

高斯低通滤波器的传递函数为：

HLP(u,v)=e−D2(u,v)/2σ2H_{LP}(u,v)=e^{-D^2(u,v)/2\sigma^2}

则高斯高通滤波器传递函数为：

HHP=1−HLP(u,v)=1−e−D2(u,v)/2D02H_{HP}=1-H_{LP}(u,v)=1-e^{-D^2(u,v)/2D_0^2}

其中， D(u,v)D(u,v) 为中心点到任一点的距离， D0D_0 为设置半径。

代码（DFT代码文件见最后）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 高斯高通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径
    float h, d;        // h 为计算量，d 为到中心点的距离

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = 1 - exp(-d / (2.0 * r * r));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

r=120

巴特沃斯高通滤波

巴特沃斯高铁滤波器的传递函数为：

H(u,v)=11+[D0/D(u,v)]2nH(u,v)=\frac {1} {1+[D_0/D(u,v)]^{2n} }

其中， D(u,v)D(u,v) 是P×Q频率矩形中心到矩形中包含的任意一点(u,v)的距离， D0D_0 是截止频率（设置半径）， nn 是巴特沃斯滤波器的阶数。

代码（DFT代码文件见最后）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    // 巴特沃斯高通滤波
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 120;    // 滤波半径
    float h, d;        // h 为计算量，d为到中心点的距离
    float n = 3;    // 巴特沃斯滤波器阶数

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = 1.0 / (1 + pow(((r * r) / d), 2 * n));
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

r=120,n=3

拉普拉斯滤波

频率域中拉普拉斯滤波传递函数为：

H(u,v)=−4π2(u2+v2)=−4π2[(u−P/2)2+(v−Q/2)2]=−4π2D2(u,v)H(u,v)=-4\pi^2(u^2+v^2)=-4\pi^2[(u-P/2)^2+(v-Q/2)^2]=-4\pi^2D^2(u,v)

其中， D(u,v)D(u,v) 为中心点到任一点的距离。

具体增强实现：

g(x,y)=f(x,y)+c∇2f(x,y),∇2f(x,y)=ℑ−1[H(u,v)F(u,v)]g(x,y)=f(x,y)+c\nabla^2f(x,y),\nabla^2f(x,y)=\Im^{-1}[H(u,v)F(u,v)]

其中， F(u,v)F(u,v) 是 f(x,y)f(x,y) 的傅里叶变换。

代码：

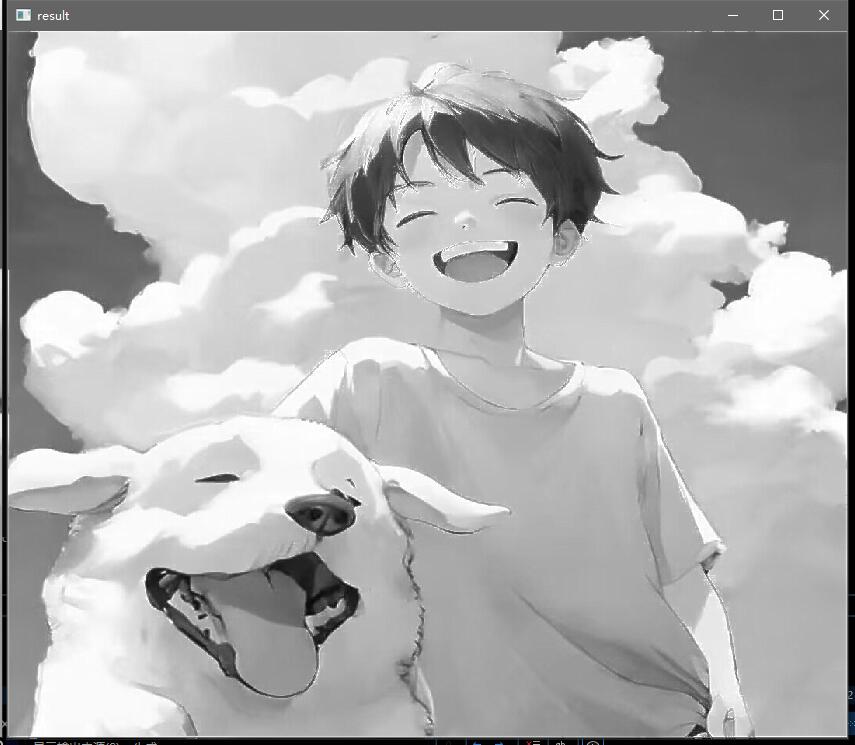
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    DFT(image, output, trf);    // 对图像进行傅里叶变换

    /*————————————————————————————拉普拉斯滤波————————————————————————————*/
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    float h, d;        // h 为计算量，d为到中心点的距离
    float pi = 3.1415926;

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = -4 * pi * pi * d;
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);

    /*————————————————————————————标记，实现g(x,y)————————————————————————————*/
    iDft[0].convertTo(iDft[0], CV_8U, 255 / 1.0, 0);
    cv::Mat result(iDft[0].size(), CV_8U);
    for (int i = 0; i < iDft[0].rows; i ++)
        for (int j = 0; j < iDft[0].cols; j ++)
            result.at<uchar>(i, j) = cv::saturate_cast<uchar>(image.at<uchar>(i, j) + iDft[0].at<uchar>(i, j));

    cv::namedWindow("result", cv::WINDOW_NORMAL);
    cv::imshow("result", result);
    cv::waitKey(0);

    return 0;
}

效果展示：

标定到原图，即g(x,y)

高频强调滤波器

还可以设置可调参数，进行调整影响。高频强调滤波的通用公式是：

g(x,y)=ℑ−1{[k1+k2HHP]F(u,v)}g(x,y)=\Im^{-1}\bigg\{\big[k_1+k_2H_{HP}\big]F(u,v)\bigg\}

其中， k1≥0k_1\geq0 偏移传递函数的值，以便使直流项不为零， k2>0k_2>0 控制高频的贡献， HHPH_{HP} 为高通滤波器传递函数， F(u,v)F(u,v) 为图像 f(u,v)f(u,v) 的傅里叶变换。

部分代码示例：

1
2
3
4
5
6
7
8
9
for (int i = 0; i < trf_real.rows; i ++)
    for (int j = 0; j < trf_real.cols; j ++)
    {
        d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
        // 高斯高频强调滤波器
        h = 0.5 + 0.75 * (1 - exp(-d / (2.0 * r * r)));
        trf_real.at<float>(i, j) *= h;
        trf_imag.at<float>(i, j) *= h;
    }

附DFT代码

1
2
3
4
5
6
// DFT.h
#pragma once
#include <opencv2/opencv.hpp>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// DFT.cpp
#include "DFT.h"

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr)
{
    // 扩展图像，优化速度
    int n = cv::getOptimalDFTSize(input.rows);
    int m = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, n - input.rows, 0, m - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 用于存储傅里叶变换的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(), CV_32F) };

    cv::merge(planes, 2, trf_arr);

    cv::dft(trf_arr, trf_arr);

    cv::split(trf_arr, planes);
    cv::Mat trf_img_real = planes[0];
    cv::Mat trf_img_imag = planes[1];

    // 计算复数的幅值，保存在output中
    cv::magnitude(planes[0], planes[1], output);

    // 优化幅值大小
    output += cv::Scalar(1);
    log(output, output);
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);

    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    int cx = output.cols / 2, cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy)), q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy)), q3(output, cv::Rect(cx, cy, cx, cy));
    cv::Mat tmp;

    // 交换区域使得原点位于中心
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

    // 复数的实数部分交换
    cv::Mat q00(trf_img_real, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q01(trf_img_real, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q02(trf_img_real, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q03(trf_img_real, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q00.copyTo(tmp); q03.copyTo(q00); tmp.copyTo(q03);        //左上与右下进行交换
    q01.copyTo(tmp); q02.copyTo(q01); tmp.copyTo(q02);        //右上与左下进行交换

    // 复数的虚数部分交换
    cv::Mat q10(trf_img_imag, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q11(trf_img_imag, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q12(trf_img_imag, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q13(trf_img_imag, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q10.copyTo(tmp); q13.copyTo(q10); tmp.copyTo(q13);        //左上与右下进行交换
    q11.copyTo(tmp); q12.copyTo(q11); tmp.copyTo(q12);        //右上与左下进行交换

    planes[0] = trf_img_real;
    planes[1] = trf_img_imag;
    cv::merge(planes, 2, trf_arr);    // 将傅里叶变换的复数结果保存在trf_arr
}

同态滤波

通过一个滤波器传递函数H(u,v)，使用不同可控方法影响低频分量和高频分量。

基本原理

图像f(x,y)可以表示为其照射分量i(x,y)和反射分量r(x,y)的乘积。

图像中，认为低频分量与照射分量相联系，高频分量与反射分量相联系。

f(x,y)=i(x,y)r(x,y)f(x,y)=i(x,y)r(x,y)

乘积的傅里叶变换不是傅里叶变换的乘积。

ℑ[f(x,y)]≠ℑ[i(x,y)]ℑ[r(x,y)]\Im [f(x,y)] \neq \Im[i(x,y)]\Im[r(x,y)]

故令 z(x,y)=ln⁡f(x,y)=ln⁡i(x,y)+ln⁡r(x,y)z(x,y)=\ln f(x,y)=\ln i(x,y)+\ln r(x,y) ，有

ℑ[z(x,y)]=ℑ[ln⁡f(x,y)]=ℑ[ln⁡i(x,y)]+ℑ[ln⁡r(x,y)]\Im[z(x,y)]=\Im[\ln f(x,y)]=\Im[\ln i(x,y)]+\Im[\ln r(x,y)]

Z(u,v)=Fi(u,v)+Fr(u,v)Z(u,v)=F_i(u,v)+F_r(u,v)

其中， Fi(u,v)F_i(u,v) 和 Fr(x,y)F_r(x,y) 分别是 ln⁡i(x,y)\ln i(x,y) 和 ln⁡r(x,y)\ln r(x,y) 的傅里叶变换。

使用滤波器传递函数 H(u,v)H(u,v) 对 Z(u,v)Z(u,v) 滤波，有

S(u,v)=H(u,v)Z(u,v)=H(u,v)Fi(u,v)+H(u,v)Fr(u,v)S(u,v)=H(u,v)Z(u,v)=H(u,v)F_i(u,v)+H(u,v)F_r(u,v)

空间域中滤波后的图像是

s(x,y)=ℑ−1[S(u,v)]=ℑ−1[H(u,v)Fi(u,v)]+ℑ−1[H(u,v)Fr(u,v)]s(x,y)=\Im^{-1}[S(u,v)]=\Im^{-1}[H(u,v)F_i(u,v)]+\Im^{-1}[H(u,v)F_r(u,v)]

最后通过取滤波后的结果的指数形成输出图像

g(x,y)=es(x,y)=eℑ−1[H(u,v)Fi(u,v)]eℑ−1[H(u,v)Fr(u,v)]g(x,y)=e^{s(x,y)}=e^{\Im^{-1}[H(u,v)F_i(u,v)]}e^{\Im^{-1}[H(u,v)F_r(u,v)]}

记

i0(x,y)=ei′(x,y)=eℑ−1[H(u,v)Fi(u,v)]i_0(x,y)=e^{i'(x,y)}=e^{\Im^{-1}[H(u,v)F_i(u,v)]}

为输出图像的照射分量，

记

r0(x,y)=er′(x,y)=eℑ−1[H(u,v)Fr(u,v)]r_0(x,y)=e^{r'(x,y)}=e^{\Im^{-1}[H(u,v)F_r(u,v)]}

为输出图像的反射分量。

上述滤波方法过程如下图：

同态滤波步骤

以高斯高通滤波器举例

一般高斯高通滤波器函数：

H(u,v)=1−e−D2(u,v)/2D02H(u,v)=1-e^{-D^2(u,v)/2D^2_0}

函数图像

使用稍微变化的GHPF（Gaussian high-pass filter）：

H(u,v)=(γH−γL)[1−e−cD2(u,v)/D02]+γLH(u,v)=(\gamma_H-\gamma_L)\big[1-e^{-cD^2(u,v)/D_0^2}\big]+\gamma_L

其中，D(u,v)D(u,v) 为中心点到任一点的距离， D0D_0 为设置半径， γL\gamma_L 和 γH\gamma_H 为规定频率范围，常数c控制函数的偏斜度，类似于高频强调函数。

变化后的GHPF图像如下：

函数图像

明显地，减少了低频分量的影响，增加了高频分量的影响。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// main.cpp
#include <iostream>
#include <opencv2/opencv.hpp>
#include "DFT.h"

int main()
{
    cv::Mat image, output, trf;
    image = cv::imread("src/test.jpg", 0);

    cv::namedWindow("before", cv::WINDOW_NORMAL);
    cv::imshow("before", image);    // 显示原图

    /* ——————————对数变换—————————— */
    cv::Mat image_(image.size(), CV_32F);
    for (int i = 0; i < image.rows; i ++)
        for (int j = 0; j < image.cols; j ++)
            image_.at<float>(i, j) = log(image.at<uchar>(i, j) + 0.1);

    DFT(image_, output, trf);    // 对图像进行傅里叶变换

    /* ——————————滤波—————————— */
    cv::Mat planes[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::split(trf, planes);    //分离通道，获取实部虚部

    cv::Mat trf_real = planes[0];
    cv::Mat trf_imag = planes[1];

    int cx = trf_real.rows / 2;    // 求中心坐标x
    int cy = trf_real.cols / 2;    // 求中心坐标y
    int r = 10;    // 滤波半径
    float h, d;        // h 为计算量，d 为到中心点的距离
    float rh = 3, rl = 0.5, c = 5;    // 高频点、低频点、c值

    for (int i = 0; i < trf_real.rows; i ++)
        for (int j = 0; j < trf_real.cols; j ++)
        {
            d = (i - cx) * (i - cx) + (j - cy) * (j - cy);
            h = (rh - rl) * (1 - exp(-c * d / (r * r))) + rl;
            trf_real.at<float>(i, j) *= h;
            trf_imag.at<float>(i, j) *= h;
        }

    planes[0] = trf_real;
    planes[1] = trf_imag;
    cv::Mat trf_ilpf;
    cv::merge(planes, 2, trf_ilpf);

    cv::Mat iDft[] = { cv::Mat_<float>(output), cv::Mat::zeros(output.size(), CV_32F) };
    cv::idft(trf_ilpf, trf_ilpf);    // 傅里叶逆变换
    cv::split(trf_ilpf, iDft);        // 分离通道
    cv::magnitude(iDft[0], iDft[1], iDft[0]);    //计算复数的幅值，保存在iDft[0]
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    /* ——————————指数恢复数值并归一化—————————— */
    cv::exp(iDft[0], iDft[0]);
    cv::normalize(iDft[0], iDft[0], 0, 1, cv::NORM_MINMAX);

    iDft[0].convertTo(iDft[0], CV_8U, 255 / 1.0, 0);
    cv::namedWindow("after", cv::WINDOW_NORMAL);
    cv::imshow("after", iDft[0]);
    cv::waitKey(0);

    return 0;
}

效果展示：

1
2
3
4
5
6
// DFT.h
#pragma once
#include <opencv2/opencv.hpp>
#include <cmath>

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// DFT.cpp
#include "DFT.h"

void DFT(cv::Mat input, cv::Mat& output, cv::Mat& trf_arr)
{
    // 扩展图像，优化速度
    int n = cv::getOptimalDFTSize(input.rows);
    int m = cv::getOptimalDFTSize(input.cols);
    cv::copyMakeBorder(input, input, 0, n - input.rows, 0, m - input.cols, cv::BORDER_CONSTANT, cv::Scalar::all(0));

    // 用于存储傅里叶变换的实部和虚部
    cv::Mat planes[] = { cv::Mat_<float>(input), cv::Mat::zeros(input.size(), CV_32F) };

    cv::merge(planes, 2, trf_arr);

    cv::dft(trf_arr, trf_arr);

    cv::split(trf_arr, planes);
    cv::Mat trf_img_real = planes[0];
    cv::Mat trf_img_imag = planes[1];

    // 计算复数的幅值，保存在output中
    cv::magnitude(planes[0], planes[1], output);

    // 优化幅值大小
    output += cv::Scalar(1);
    log(output, output);
    cv::normalize(output, output, 0, 1, cv::NORM_MINMAX);

    output = output(cv::Rect(0, 0, output.cols & -2, output.rows & -2));

    int cx = output.cols / 2, cy = output.rows / 2;
    cv::Mat q0(output, cv::Rect(0, 0, cx, cy)), q1(output, cv::Rect(cx, 0, cx, cy));
    cv::Mat q2(output, cv::Rect(0, cy, cx, cy)), q3(output, cv::Rect(cx, cy, cx, cy));
    cv::Mat tmp;

    // 交换区域使得原点位于中心
    q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);
    q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);

    // 复数的实数部分交换
    cv::Mat q00(trf_img_real, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q01(trf_img_real, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q02(trf_img_real, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q03(trf_img_real, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q00.copyTo(tmp); q03.copyTo(q00); tmp.copyTo(q03);        //左上与右下进行交换
    q01.copyTo(tmp); q02.copyTo(q01); tmp.copyTo(q02);        //右上与左下进行交换

    // 复数的虚数部分交换
    cv::Mat q10(trf_img_imag, cv::Rect(0, 0, cx, cy));        // 左上区域
    cv::Mat q11(trf_img_imag, cv::Rect(cx, 0, cx, cy));        // 右上区域
    cv::Mat q12(trf_img_imag, cv::Rect(0, cy, cx, cy));        // 左下区域
    cv::Mat q13(trf_img_imag, cv::Rect(cx, cy, cx, cy));    // 右下区域
    q10.copyTo(tmp); q13.copyTo(q10); tmp.copyTo(q13);        //左上与右下进行交换
    q11.copyTo(tmp); q12.copyTo(q11); tmp.copyTo(q12);        //右上与左下进行交换

    planes[0] = trf_img_real;
    planes[1] = trf_img_imag;
    cv::merge(planes, 2, trf_arr);    // 将傅里叶变换的复数结果保存在trf_arr
}
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。